Статистическая значимость: что это на самом деле, как считать и какие ошибки допускают при ее оценке
Маркетолог запустил две версии рекламной рассылки. Версия А получила на 5% больше кликов, чем версия B. Руководство спрашивает: «Это победа? Можно ли доверять разнице?». Или ученый провел эксперимент с новым препаратом. У пациентов в тестовой группе улучшения чуть заметнее. Это доказательство эффективности или случайная удача?
Содержание
Нужен способ отделить реальные прорывы от статистического шума. Способ понять, что разнице можно доверять, и она возникла не случайно. Для этого существует концепция статистической значимости — фильтр, который помогает принимать обоснованные решения в мире, полном неопределенности.

В этой статье мы разберем, что это на самом деле, как работает, как проверить ее на практике и какие распространенные ошибки искажают результаты, лишая даже впечатляющие цифры доказательной силы.
Что такое статистическая значимость и p-value простыми словами
Предположим, вы управляете интернет-магазином одежды и хотите увеличить продажи. Дизайнеры изменили цвет кнопки «Купить» с синего на зеленый. Для оценки изменений вы запускаете A/B-тест: одна половина посетителей видит синюю кнопку, другая — зеленую.

Через две недели:
- синяя кнопка дает конверсию в покупку — 4,1%;
- зеленая кнопка — 4,5%.
Разница в 0,4 процентных пункта — это реальный успех зеленой кнопки или случайный результат? Возможно, в группе с зеленой кнопкой просто было больше клиентов, готовых к покупке. Если вы примете решение без статистического анализа, можно потратить ресурсы на неэффективное изменение.
Нужно узнать, если бы на самом деле разницы между кнопками не было, какова вероятность получить в эксперименте расхождение в 0,4% или даже больше? Ответить на этот вопрос поможет конкретная метрика.
P-value в статистике — оценка вероятности увидеть эффект там, где его нет. Это число всегда находится в диапазоне от 0 до 1.
Рассмотрим два значения.
- 0,03 означает: «Шанс случайно увидеть такой результат составляет всего 3%». Маловероятно.
- 0,45 означает: «Вероятность получить такую разницу просто по воле случая — 45%». Вполне обычное дело.
Чем ниже p-value, тем меньше вероятность, что результат — случайность. Но важно помнить, что низкий показатель еще не значит, что зеленая кнопка действительно лучше.
Статистическая значимость — это решение, основанное на p-value. Мы заранее устанавливаем порог доверия (уровень значимости), обычно α = 0,05 (5%).
Правило
- Если p-value ≤ α (например, 0,03 ≤ 0,05), результат считается статистически значимым. То есть разница в данных, скорее всего, не случайна.
- Если p-value > α (например, 0,45 > 0,05), то результат считается статистически незначимым. То есть разница может быть случайной.
Если вы хотите научиться применять методы статистического анализа на практике, запишитесь на курс «Аналитик данных». За пять с половиной месяцев вы сможете освоить навыки, которые востребованы в разных сферах, от e-commerce до медиа.
Фундамент: гипотезы и уровень значимости
Перед тем, как принять решение, нужно оценить, насколько полученные данные могут быть случайными. Это невозможно без понимания таких основ статистики, как гипотезы и уровень значимости. В этом разделе мы расскажем, как нулевая и альтернативная гипотезы определяют ваши исходные предположения, а уровень значимости и доверительный интервал помогают проверить их с научной точки зрения.
Нулевая (H0) и альтернативная (H1) гипотезы
Проверка значимости начинается с формулировки двух противоположных утверждений.
Нулевая гипотеза (H0) — это исходное предположение о том, что эффекта, разницы или взаимосвязи не существует. Мы считаем, что все наблюдаемые отклонения случайны.
Пример H0: Конверсия зеленой кнопки равна конверсии синей кнопки. То есть смена цвета не влияет на поведение покупателей.
Альтернативная гипотеза (H1) — предположение о существовании эффекта или различия, которое мы пытаемся подтвердить с помощью данных.
Пример H1: Конверсия зеленой кнопки не равна конверсии синей кнопки. Это означает, что разница в 0,4% — не случайность, а реальное влияние цвета.
Вот примеры подобных утверждений в других областях.
| Область | Нулевая гипотеза (H0) | Альтернативная гипотеза (H1) |
| Промышленность | Изменение параметра на производственной линии не влияет на количество бракованных изделий | Изменение параметра снижает процент брака |
| Политология | Уровень поддержки кандидата А не изменился после предвыборных дебатов | Уровень поддержки кандидата А вырос после дебатов |
| Machine Learning | Новая модель машинного обучения не превосходит текущую по точности предсказаний | Новая модель превосходит текущую по точности |
Нулевая гипотеза (H0) почти всегда консервативна и утверждает, что изменений, эффекта или различий нет. Мы требуем от данных убедительных доказательств, чтобы отклонить это предположение и принять альтернативу (H1), в которой заложена идея нового знания или открытия. Этот принцип лежит в основе любого строгого статистического тестирования.
Уровень значимости (Alpha) и доверительный интервал
Мы уже знаем, что уровень значимости (α) — это порог, с которым сравнивают p-value, чтобы вынести решение. Но откуда он берется?
Представьте, что вы — специалист по контролю качества на заводе. Установлено правило: если в случайной проверке партии брак составляет более 5%, всю партию отклоняют. Эти 5% — ваш риск забраковать хорошую партию из-за случайности.
Аналогично, α — это предел терпимости к ошибке первого рода, то есть к тому, что мы ошибочно отвергнем нулевую гипотезу, когда она верна. Устанавливая α = 0,05, мы говорим: «Мы готовы в 5% случаев ошибочно заявить об эффекте, которого нет».
Уровень значимости и доверительный интервал — два аспекта одного процесса. Они связаны.
уровень доверия = (1 – α) × 100%
Если α = 0,05, то уровень доверия — 95%.
Вернемся к примеру с интернет-магазином. Мы увидели, что зеленая кнопка увеличивает конверсию на 0,4%. Но насколько точен этот результат? Если повторить тест, итог может немного измениться.
Доверительный интервал помогает понять, в каком диапазоне с заданной уверенностью находится реальный эффект. Как он рассчитывается? Статистические методы оценивают возможную погрешность нашей цифры 0,4% на основе двух ключевых факторов:
- объема данных (сколько посетителей участвовало в тесте),
- естественного разброса (насколько стабильна конверсия изо дня в день).
Если данных много и конверсия стабильна, погрешность мала, и интервал будет узким, например, [0,3%; 0,5%]. Это высокая точность.
Если данных мало или они очень изменчивы, погрешность велика, и интервал окажется широким, например, [-0,2%; +1,0%]. Неопределенность высока, и мы даже не можем исключить отсутствие эффекта.
В нашем случае, для разницы в 0,4% рассчитали 95% доверительный интервал, от +0,1% до +0,7%. Это означает, что, хотя точечная оценка — 0,4%, мы на 95% уверены, что истинный эффект лежит где-то в этом диапазоне. Если бы мы хотели быть более строгими и снизили риск ошибки до α = 0,01, то наш доверительный интервал стал бы 99%, но при этом он был бы шире (например, от -0,1% до +0,9%), так как требование к точности возрастает.

Два способа сделать статистический вывод
Как рассчитать и проверить статистическую значимость
Проверка статистической значимости — это последовательный алгоритм из нескольких шагов, который подходит для большинства задач, от A/B-тестов до исследований.
Шаг 1. Сформулируйте гипотезы
Начните с четкой постановки утверждений:
- H0 — эффекта нет.
- H1 — эффект есть.
Шаг 2. Соберите данные и выберите тест
Проведите эксперимент или используйте готовые данные. Затем выберите статистический критерий, который зависит от типа данных и задачи:
- для сравнения средних — t-тест;
- для сравнения долей (конверсий) — z-тест или хи-квадрат;
- для нескольких групп или факторов — ANOVA, регрессия и др.
Шаг 3. Задайте уровень значимости (α)
Заранее установите допустимый риск ошибки. Обычно используют α = 0,05 — это означает готовность в 5% случаев ошибочно обнаружить эффект там, где его нет.
Шаг 4. Рассчитайте p-value
Это технический шаг, который можно выполнить с помощью различных инструментов и библиотек для анализа данных. Например:
- Google Analytics — в A/B-тестах на веб-сайтах часто используется встроенная функция расчета p-value.
- Excel или Google Sheets — можно использовать функцию T.TEST или Z.TEST для стандартных t-тестов и z-тестов.
- Python — с помощью библиотеки SciPy можно рассчитать p-value для большинства статистических тестов.
- R — есть готовые функции для расчета этого показателя, такие как t.test() или prop.test() для анализа пропорций.
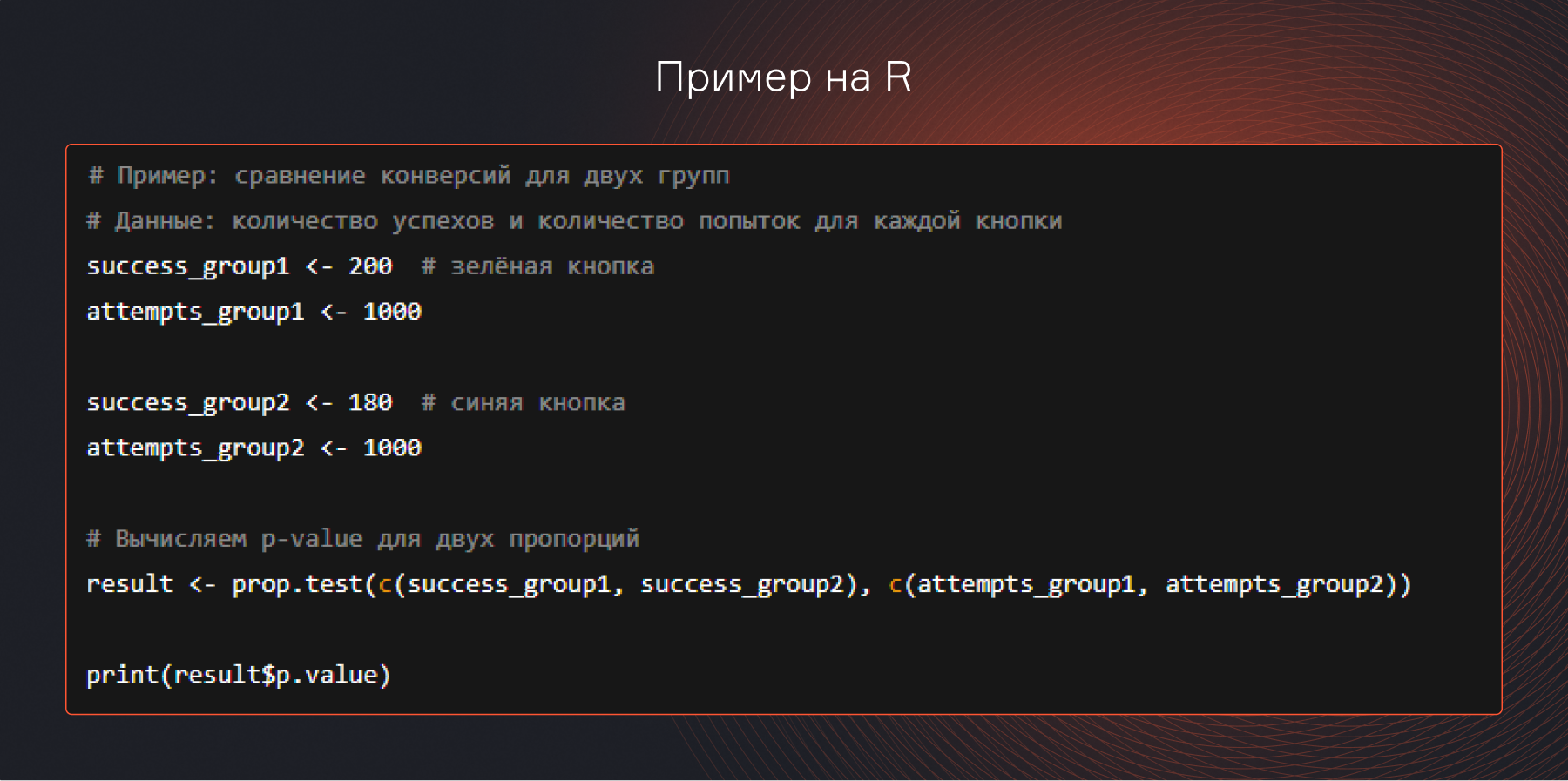
Шаг 5. Примите решение
Сравните p-value с α:
- ≤ α (0,03 ≤ 0,05) — такие данные маловероятны, если H0 верна, поэтому ее отвергаем.
- > α (0,15 > 0,05) — результат незначим, доказательств против H0 недостаточно.
Важно
Незначимый результат не равен тому, что эффекта нет. Возможно, эксперимент был слишком коротким или выборка слишком мала.
Помимо вердикта «значимо — незначимо», всегда анализируйте доверительный интервал. Он показывает, насколько велик эффект и с какой точностью он оценен. Даже статистически значимый результат может быть практически бесполезным, если эффект слишком мал.
Инструменты считают за вас, но корректная формулировка гипотез и грамотная интерпретация результата всегда остаются задачей человека.

Примеры оценки значимости в реальных задачах
Концепция статистической значимости — необходимый инструмент в работе аналитика, маркетолога, ученого. Давайте рассмотрим три ситуации, где она играет ключевую роль.
Пример 1. Продуктовый анализ — A/B-тест новой функции
Команда мобильного приложения банка добавила возможность быстрого перевода по номеру телефона на главный экран (новая версия «B»). Нужно понять, увеличивает ли это изменение общее число переводов по сравнению со старым интерфейсом (версия «A»).
Гипотезы:
- H0 — среднее число переводов на пользователя в версии A равно среднему числу в версии B.
- H1 — среднее число переводов на пользователя в версиях A и B различается.
Аналитик запускает тест, собирает данные за две недели. Используя t-тест для независимых выборок, он получает p-value = 0.01.
Поскольку 0.01 < 0.05, результат статистически значим. Нулевая гипотеза отвергается. С уверенностью 95% можно заявить, что новая функция действительно повлияла на поведение пользователей, и ее стоит выпускать на всех пользователей.
Дополнительно аналитик смотрит на доверительный интервал для разности средних, чтобы оценить размер эффекта в денежном выражении.
Чтобы освоить полный пайплайн A/B-тестирования, попробуйте «Симулятор A/B-тестов». Этот тренажер подойдет специалистам любого уровня, содержит много практических заданий и курируется экспертами IT-индустрии.
Пример 2. Оценка эффективности рекламной кампании
Компания запустила таргетированную рекламу в новом регионе. Нужно оценить, привела ли рекламная кампания к статистически значимому росту узнаваемости бренда по сравнению с контрольным регионом, где рекламы не было.
Гипотезы:
- H0 — доля людей, узнавших бренд, в тестовом регионе равна доле в контрольном регионе.
- H1 — доля людей, узнавших бренд, в тестовом регионе выше, чем в контрольном.
Проводится опрос в двух регионах. Аналитик использует z-тест для сравнения двух долей. Рассчитанное p-value = 0.2.
Поскольку 0.2 > 0.05, результат статистически незначим. Недостаточно доказательств, чтобы утверждать, что кампания повысила узнаваемость. Возможно, эффект был слишком мал, или выборка опроса недостаточно велика. Это сигнал для маркетологов: либо увеличивать бюджет и охват для более заметного эффекта, либо пересматривать креатив, а не считать рекламу автоматически успешной.
Пример 3. Операционная аналитика — контроль качества процесса
На производстве внедрили новую смазку для станков. Инженеры утверждают, что это снижает процент бракованных деталей. Аналитику нужно проверить это утверждение по данным за месяц до и после внедрения.
Гипотезы:
- H0 — средний процент брака после внедрения равен проценту брака до внедрения.
- H1 — средний процент брака после внедрения ниже, чем до.
Аналитик собирает ежедневные данные о проценте брака. Для связанных измерений (одна и та же линия до и после) он применяет парный t-тест. Результат: p-value = 0.001.
Вывод: 0.001 << 0.05. Разница очень значима. С высокой степенью уверенности можно заключить, что новая смазка действительно улучшила качество продукции. Это решение позволяет масштабировать изменение на все станки, опираясь не на мнение, а на данные.
Типичные ошибки при оценке статистической значимости
- Игнорировать проверку предположений теста
Статистические тесты требуют определенных условий (нормальность, однородность дисперсий). Применение тестов без проверки этих условий может привести к ошибкам.
Как избежать: проведите разведочный анализ данных (EDA) и, если нужно, используйте непараметрические тесты.
- Проблема множественного тестирования
При множественных сравнениях шанс случайно получить значимый результат возрастает.
Как избежать: используйте поправки (например, Бонферрони) или проводите тесты поэтапно.
- Путать статистическую значимость с практической важностью
Получение статистически значимого результата (p-value < 0.05) не всегда означает, что эффект значителен для бизнеса. Например, увеличение конверсии на 0.001% не оправдает затраты бизнеса на внедрение изменений.
Как избежать: обратите внимание на доверительный интервал и оцените, действительно ли эффект полезен.
- Неправильная интерпретация p-value
Метрика не говорит о вероятности нулевой гипотезы. Это вероятность данных при условии, что нулевая гипотеза верна.
Как избежать: Помните, что p-value измеряет неожиданность данных, а не вероятность гипотезы.
- Прекращать тест сразу после достижения значимости
Остановка теста, как только p-value падает ниже 0.05, может привести к ложным выводам из-за недостаточности данных.
Как избежать: Определите заранее размер выборки и продолжительность теста. Используйте последовательные схемы тестирования, если нужно остановить эксперимент раньше.
Заключение
В статье мы выяснили, что p-value — это вероятность, что полученные результаты могли бы возникнуть случайно, если эффекта нет. Статистическая значимость — это решение, которое мы принимаем, сравнивая p-value с заранее установленным порогом (α).
Но самый важный момент — это интерпретация результатов. Статистически значимый результат не означает, что эффект полезен для бизнеса. Он просто говорит, что эффект, скорее всего, существует.
Прежде чем делать выводы или менять что-то на основе тестов, задайте себе эти вопросы:
- Что говорит доверительный интервал? Возможно, его минимальная величина слишком мала.
- Имеет ли эффект практическую ценность? Например, изменение на 0,1% может вообще не повлиять на бизнес.
- Все ли условия соблюдены? Нет ли ошибки?
Используйте статистику как фильтр для идей, но не забывайте, что окончательное решение всегда за вами. Статистика помогает принять решение, но следовать ли ему — зависит от здравого смысла.
