Регрессионный анализ — что это такое простыми словами, примеры модели и задачи регрессии
Если вы когда-нибудь задумывались, сколько топлива расходует автомобиль в зависимости от скорости движения, или пытались предсказать срок службы вентилятора по тому, как часто он используется, — вы уже интуитивно касались темы регрессии. В этой статье объясним, что такое регрессионный анализ в статистике простыми словами, как он помогает находить связи между числами, делать прогнозы и принимать решения на основе данных.
Содержание
- Определение метода
- Зачем это нужно
- Чем регрессия отличается от корреляции
- Основные термины
- Методы регрессионного анализа
- Условия применения регрессионного анализа
- Применение
- Этапы проведения
- Преимущества и недостатки регрессионного анализа
- Пример
- Как применять регрессионный анализ в Data Science
- Подведем итоги

Определение метода
Представьте, что хотите спрогнозировать, сколько времени потребуется, чтобы доехать до работы. Нужно понять, как на длительность маршрута влияет расстояние от дома до офиса и время, в которое вы выезжаете.
Логично, что чем дальше ехать — тем дольше. А если вы попали в утренний час пик, дорога к рабочему месту становится еще длиннее. Можно записывать поездки каждый день и отмечать определенные закономерности между этими факторами. Исследовать возникающие связи поможет статистический метод, который объясняет, как разные переменные влияют на результат.
Регрессионное моделирование и анализ данных с использованием регрессии позволяют построить формулу, по которой можно предсказывать время в пути в зависимости от расстояния и времени выезда. Такая модель учится на предыдущих поездках и потом может делать прогнозы для новых ситуаций — например, сказать, сколько примерно займет дорога, если вы выедете в 8 утра и ехать вам 12 километров.
Зачем это нужно
Всё начинается с вопроса, как один параметр влияет на другой? Необходимо не просто предсказать числа, а понять, от чего зависит результат и как на него можно повлиять. Понимание взаимосвязей между переменными — вот основная цель регрессионного анализа, и задачи метода проистекают из нее:
- Прогнозирование. Например, вы знаете, сколько компания тратит на рекламу и какие получает продажи. На основе этого можно прикинуть, сколько получится заработать в следующем месяце, если увеличить или уменьшить рекламный бюджет.
- Поиск зависимостей. С помощью инструмента мы разбираемся в том, что влияет на результат. Допустим, вы хотите понять, что сильнее привлекает покупателей в вашем магазине: удобное местоположение, часы работы или качество обслуживания. Регрессия покажет, какой фактор играет главную роль. Например, может оказаться, что продлить работу на час вечером выгоднее, чем открываться раньше утром.
- Принятие решений и оптимизация. Понимать, как разные параметры влияют на результат, чтобы не гадать, а действовать осознанно. Вы продаёте товар онлайн. Что будет, если снизить цену на 10%? Если расчеты показывают, что это приведёт к росту продаж на 20%, — это уже не интуиция, а основание для решения.
- Проверка гипотез. Например, вы думаете, что повышение цены на 5% снизит спрос. Загружаете в формулу данные о прошлых ценах и продажах — и получаете ответ: да, снижение есть, но только если цена вырастет на 10%. Гипотезу стоит скорректировать.
Чем регрессия отличается от корреляции
Если вы только начинаете разбираться в Data Science, спутать эти понятия очень легко. И там, и там речь идёт о связях между переменными. Но есть важное отличие.
Корреляционный анализ показывает, есть ли связь между двумя вещами и насколько сильная. Но он не говорит, что на что влияет. Просто указывает: эти два показателя движутся вместе — например, чем выше температура, тем больше продаётся мороженого.
Иногда нужен метод, который как бы отвечает на вопрос: «А что произойдет, если я изменю вот это?» Допустим, на сколько вырастут продажи освежающих напитков, если на улице потеплеет на 5 градусов.
Регрессия в статистике простыми словами — это способ понять, как одна величина влияет на другую, и использовать эти знания, чтобы предсказывать и принимать решения. А корреляция — просто наблюдение.
Основные термины
Чтобы не запутаться в предмете статьи еще больше, давайте разберемся с базой. Терминологии здесь немного.
- Зависимая переменная (Y) — то, что мы хотим предсказать. Например, средний балл студента (GPA).
- Независимая переменная (X) — то, от чего зависит результат. Например, сколько часов в неделю занимается студент.
- Коэффициенты — это числа, которые показывают, как сильно X влияет на Y. Допустим, если коэффициент равен 0,3, значит каждый дополнительный час занятий добавляет 0,3 балла к среднему.
- Уравнение регрессии — в статистике это формула связи. Например:
GPA = 2,0 + 0,3 × часы в неделю
Здесь 2,0 — стартовый балл, а 0,3 — прибавка за каждый час.
- R-квадрат (коэффициент детерминации) — показывает, насколько модель вообще полезна. Если он равен 0,8, значит 80% изменений в среднем балле можно объяснить количеством учебы. Чем ближе к 1 — тем лучше.
Методы регрессионного анализа
Каждый перечисленный ниже подход — просто инструмент, который помогает решать разные практические задачи. Типы и модели регрессии могут быть разными, но логика у них похожая: понять, как одни данные влияют на другие. Для наглядности, в конце блока представим сравнительную таблицу.
Линейная регрессия
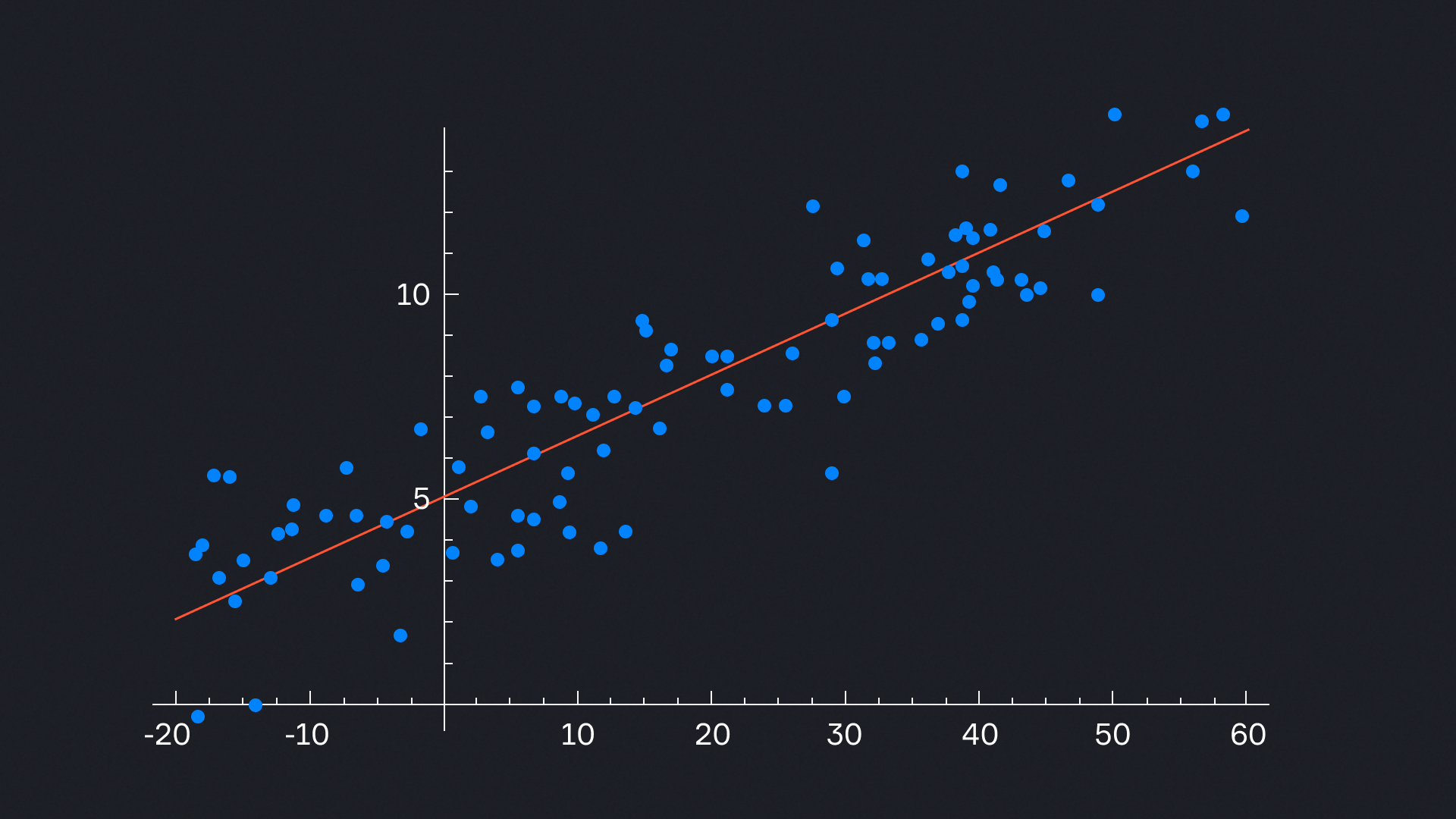
Самый базовый и понятный вариант. Здесь есть одна причина (X) и один результат (Y), и между ними — прямая линия. Например, чем больше опыта у сотрудника, тем выше зарплата. Эта модель хорошо подходит для простых зависимостей, которые можно изобразить прямой.
Множественная линейная регрессия
Этот метод используется, когда причин несколько. Например, на стоимость машины влияет и её пробег, и год выпуска, и марка. Модель учитывает все эти факторы сразу и помогает точнее предсказывать результат.
Полиномиальная регрессия
Иногда связь между переменными — не прямая, а закрученная. Например, производительность может сначала расти, а потом снижаться. Тогда вместо прямой линии строится кривая — полиномиальная. Такой подход ловит более сложные зависимости. Представим, что вы хотите выяснить, сколько часов сна нужно, чтобы быть максимально продуктивным в течение дня.
- Если человек спит 3–4 часа, он чувствует усталость и работает хуже.
- При 7–8 часах сна — продуктивность на пике.
- А если спать по 10–11 часов, появляется вялость и снижение концентрации.
Если построить график зависимости продуктивности от количества сна, получится изогнутая линия: сначала рост, потом спад. Линейная модель не подойдет, а полиномиальная отразит эту естественную «горку».
Логистическая регрессия
Здесь результат — не число, а категория. Например: купит клиент товар или не купит, да или нет. Очень полезна в маркетинге и медицине, когда важно понять, произойдет событие или нет. Допустим, вы состоите в приемной комиссии и хотите спрогнозировать, примут ли абитуриента в университет на основе его баллов ЕГЭ.
У вас есть такие данные:
- балл по математике;
- балл по русскому языку;
- балл по профильному предмету.
Тут важно не предсказать точное число, а понять, с какой вероятностью человек поступит. Если вероятность больше определенного порога (например, 0.5), модель сможет предсказать итог.
Сравнительная таблица по основным видам
| Вид регрессии | Что предсказывает | Когда использовать | Пример |
| Линейная | Число | Есть одна причина и результат меняется линейно | Доход в зависимости от стажа |
| Множественная | Число | Есть несколько факторов, которые вместе влияют на результат | Цена квартиры в зависимости от площади, этажа и района |
| Полиномиальная | Число | Связь между данными нелинейная (например, сначала рост, потом спад) | Продуктивность работника в зависимости от нагрузки |
| Логистическая | Категорию (да/нет) | Предсказать вероятность наступления события | Купит ли человек продукт, есть ли риск болезни |
Условия применения регрессионного анализа
Прежде чем строить модель и делать выводы, важно убедиться: а можно ли вообще использовать этот способ в конкретной ситуации? Нужны определенные предпосылки. Если их не будет, алгоритм начнет «врать» или показывать странные результаты. Вот основные моменты, на которые стоит обратить внимание.
- Логичная связь между переменными.
Например, вы хотите понять, как количество тренировок влияет на выносливость. Это логично. А вот искать связь между цветом кроссовок и скоростью бега — уже странно.
- Переменные измеряются в числах.
Регрессия работает с числами. Если вы анализируете только категории (например, любимые фильмы), то нужны другие методы или предварительная подготовка данных.
- Связь между параметрами более-менее стабильна.
Если сегодня количество рекламы влияет на продажи, а завтра — нет, то построить надежную модель будет сложно.
- Нет ярко выраженных выбросов.
Один «аномальный» случай может сильно исказить результаты. Например, если в вашем наборе данных один человек заработал в 100 раз больше остальных — модель может потянуться за ним и стать неточной.
- Достаточно информации.
Чем больше наблюдений, тем надёжнее. Если вы строите прогноз по трем примерам — лучше сначала собрать больше материала.
Если эти условия соблюдены, метод даст полезные и осмысленные результаты. Если нет — лучше подумать, как подготовить метрики или выбрать другой подход.
Применение
Этот инструмент помогает находить закономерности и принимать решения в самых разных сферах. Где-то с его помощью считают доходы, где-то — прогнозируют спрос, а где-то — оценивают риски для здоровья. Давайте посмотрим, как это работает на практике. Ниже — реальные ситуации, где используется регрессионная зависимость и примеры моделей регрессии.
Экономика и финансы
Как оценить влияние уровня процентной ставки на количество выданных ипотек? Или как изменение курса доллара влияет на цену импортных товаров? С помощью героя нашей статьи. Этот инструмент позволяет прогнозировать инфляцию, цену акций, уровень безработицы, спрос на кредиты и многое другое.
Маркетинг и продажи
В этой сфере метод помогает прогнозировать продажи в зависимости от рекламного бюджета, времени года и количества промоакций. Выяснить, влияет ли оформление сайта на конверсию. Понять, что именно влияет на рост продаж, лояльность клиентов и эффективность рекламных кампаний.
Медицина и биология
Регрессия часто применяется для оценки рисков, диагностики и прогнозов развития болезней. Например, предсказать вероятность инфаркта в зависимости от возраста, давления и уровня холестерина. Или узнать, как дозировка лекарства влияет на скорость выздоровления.
Инженерия и производство
В технических задачах регрессионный анализ используется для оптимизации процессов, контроля качества и снижения издержек. Он помогает определить, как температура и влажность влияют на прочность материала. Или рассчитать, как настройки оборудования сказываются на выпуске продукции.
Спорт
В этой сфере статистический анализ зависимости помогает оценивать результаты и перспективы, а также планировать тренировки. Спрогнозировать, как количество упражнений, рацион и возраст влияют на спортивные достижения. Или — с какой вероятностью команда выиграет матч при определённой тактике.
Социология и психология
Здесь регрессионные модели описывают скрытые связи между поведением людей и различными факторами. К примеру, помогают узнать, влияет ли уровень дохода на удовлетворенность жизнью. Или выяснить, как стресс сказывается на успеваемости студентов.
Этапы проведения
Недостаточно просто «вставить данные в формулу и получить ответ». Чтобы результат был полезным и точным, важно пройти все ключевые шаги.
- Поставить цель. Понять, что вы хотите узнать. Например: «Как рекламный бюджет влияет на продажи?»
- Собрать и подготовить данные. Выбрать информацию, которая отражает вашу задачу. Затем очистить ее:
- удалить дубликаты;
- заполняются пропущенные значения;
- проверить на ошибки.
Если параметры представлены в виде категорий, их переводят в числовой вид.
- Выбрать переменные. Допустим, в задаче про продажи рекламный бюджет — независимая, продажи — зависимая.
- Построить модель. Примените выбранный метод регрессии (линейная, полиномиальная, логистическая и т. д.). Программа «учится» — и находит наилучшую зависимость между факторами.
- Проверить алгоритм. Нужно понять, насколько точны прогнозы. Смотрят на показатели вроде R-квадрат, ошибки предсказания, графики остатков. Если точность недостаточна, возвращаемся к предыдущим шагам.
- Интерпретировать результаты. Теперь можно смотреть на коэффициенты и делать выводы. Иногда это важнее самого предсказания — понять, почему что-то происходит.
- Применить программу. Если всё работает — используйте на новых сведениях: делайте прогнозы, принимайте решения, тестируйте гипотезы и стройте стратегию на будущее.
Преимущества и недостатки регрессионного анализа


Пример
Допустим, вы решили предсказать вес человека (в кг) в зависимости от параметров:
- роста (X₁) — в см;
- возраста (X₂) — в годах.
Таблица данных
| Человек | Рост (X₁), см | Возраст (X₂), лет | Вес (Y), кг |
| 1 | 160 | 25 | 58 |
| 2 | 165 | 30 | 63 |
| 3 | 170 | 35 | 68 |
| 4 | 175 | 40 | 72 |
| 5 | 180 | 45 | 77 |
Формула множественной регрессии:
Y = a + b1 * X1 + b2 * X2
После простого анализа (допустим, вы сделали расчёты в Excel или Python), получили модель:
Y = -80 + 0.5 * X1 + 0.4 * X2
Толкование коэффициентов:
- Каждые +1 см роста прибавляют 0.5 кг к весу.
- Каждые +1 год возраста прибавляют 0.4 кг.
- Свободный коэффициент – просто смещение (его смысл в данном контексте не так важен).
Прогноз: сколько будет весить человек с ростом 172 см и возрастом 33 года? Считаем.
Y = -80 + 0.5 * 172 + 0.4 * 33 = -80+86+13.2 = 19.2 кг
Кажется, что результат нереалистичный. Значит, наша модель неточна, либо влияние переменных недооценено, либо не хватает данных. Такое бывает в реальной аналитике.
Как применять регрессионный анализ в Data Science
Это простой инструмент, который легко освоить на начальном уровне. С помощью готовых библиотек, таких как scikit-learn, можно быстро построить модель и начать работать. Однако на практике могут возникнуть сложности, связанные с качеством данных, выбросами или скрытыми зависимостями. Также важно уметь интерпретировать результаты. Чтобы получить точные и осмысленные выводы, нужна практика.
Если у вас уже есть базовые знания по аналитике, запишитесь на курс «Симулятор Data Science». Здесь можно потренироваться на реальных задачах и создать проект для портфолио.
Подведем итоги
Так что же это такое — регрессионная модель? Это математическая функция, которая помогает предсказать значение зависимой переменной на основе независимых переменных. Простыми словами, это способ найти линейную или нелинейную взаимосвязь между данными и использовать её для прогнозов. Метод помогает предсказать поведение рынка, зарплату на основе опыта работы или стоимость товара. Но очень важно использовать качественную информацию, иначе итоговые расчеты будут неверными.
Вопрос-ответ
Как выглядит простой пример предсказательного алгоритма в реальной жизни?
Сеть магазинов верхней одежды анализирует ежемесячные продажи зимних пальто и обнаруживает, что чем ниже опускается температура, тем охотнее покупают товар. Используя данные за предыдущие года, можно предсказать, как сезонные тенденции влияют на предпочтения покупателей, и подготовиться к росту спроса в холодные месяцы.
Какие данные необходимы для построения модели регрессии?
Для этого нужны:
- Зависимая переменная — то, что мы хотим предсказать.
- Независимые переменные — факторы, которые влияют на результат.
- Наблюдения — конкретные случаи с информацией по всем параметрам.
Пример: если мы предсказываем цену дома, то зависимая переменная — цена, независимые — площадь, количество комнат и местоположение, а наблюдения — определенные дома со своими характеристиками.
Как оценивается ее точность?
С помощью нескольких метрик и статистических критериев:
- Коэффициент детерминации (R²) означает, насколько хорошо алгоритм объясняет изменения в данных. Чем ближе к 1, тем точнее.
- Средняя квадратичная ошибка (MSE) и средняя абсолютная ошибка (MAE) показывают, насколько ошибаются прогнозы. Чем ниже, тем точнее.
- F-критерий Фишера проверяет, насколько анализ полезен, сравнивая ошибки с реальными результатами.
- Стандартная ошибка невязки оценивает, как модель будет работать с новой информацией.



