Модель ARIMA для прогнозирования временных рядов: теория и практика на Python

Представьте, что работаете в кафе и хотите спрогнозировать, сколько посетителей придет в следующем месяце. У вас есть данные за прошлые периоды: понятно, как количество клиентов менялось в зависимости от сезона, праздников и погоды. Но как на основе этой информации построить прогноз? Для решения таких задач идеально подходит модель ARIMA.

ARIMA — это статистический метод для прогнозирования временных рядов. Эта модель анализирует исторические данные, выявляя в них устойчивые закономерности и зависимости, и использует эти паттерны для построения прогнозов.

Она востребована в самых разных областях, будь то спрос на товары, цены на акции или потребление энергии. С помощью этой модели можно относительно точно предсказать, что будет происходить в будущем, основываясь на том, что происходило в прошлом.

Основы временных рядов: тренд, сезонность и стационарность

Итак, ARIMA работает с историческими данными. Но не с любыми, а с такими, которые собраны в хронологическом порядке, например, по дням, месяцам или годам. Такой набор данных и называется временным рядом.

Вернемся к примеру с кафе. Если построить график посещаемости за несколько лет, можно заметить три основные закономерности.

• Тренд

Растет ли число гостей в долгосрочной перспективе или, наоборот, падает.

• Сезонность

Повторяющиеся колебания. Например, всплески по выходным, спад в январе или ажиотаж летом.

• Случайная составляющая

Непредсказуемые отклонения, вызванные разовыми событиями. Например, проливной дождь в какой-то выходной. 

Умение видеть и анализировать эти компоненты — ключ к пониманию того, как работает ARIMA.

Что такое стационарность 

Представьте, что пытаетесь измерить рост мальчика, который крутится на карусели. Показания будут постоянно меняться не только потому, что ребенок растет (тренд), но и из-за движения карусели. С такими данными сложно работать.

Стационарность — это статистическое свойство временного ряда, которое означает, что его основные характеристики не меняются со временем. То есть ряд не имеет тренда и сильной сезонности, он колеблется вокруг постоянного среднего уровня.

Модель ARIMA построена на предположении, что закономерности, обнаруженные в прошлом, будут устойчивы в будущем. Если данные постоянно меняются, то есть ряд нестационарный, модель даст неточные прогнозы. Она просто не будет успевать за реальными изменениями. Поэтому прежде чем строить прогноз, важно сначала превратить нестационарный ряд в стационарный. Обычно это самый первый и важный шаг.

Тест Дики-Фуллера: как проверить ряд на стационарность

Этот тест проверяет, есть ли у данных тренд, то есть изменяются ли они с течением времени. Он отвечает на вопрос: «Могли ли эти данные возникнуть случайным образом, или же есть четкое изменение?» Если тест показывает, что тренд есть, значит, ряд не стационарен, и нам нужно его преобразовать.

Допустим, вы анализируете количество клиентов в вашем кафе, и видите, что с каждым месяцем оно растет. Тест Дики-Фуллера может показать, что ваш ряд не стационарен, потому что продажи растут с каждым месяцем. Нужно применить метод, чтобы привести данные к стационарному виду.

В Python для этого есть готовая функция в библиотеке statsmodels. Выглядит это так:

Если p-значение (p-value) меньше 0.05, считаем данные стационарными. Если больше — нужно применить методы преобразования. Об этом расскажем ниже.

Разбираем ARIMA по косточкам: из чего состоит модель

Название — аббревиатура, которая расшифровывается как авторегрессионная интегрированная модель скользящего среднего. Звучит сложно, но на самом деле довольно логично. Давайте разберем ARIMA на составляющие, чтобы понять, как она работает и какую роль играет каждый компонент.

AR(p): модель авторегрессии — прогнозируем будущее на основе прошлого

Давайте разберемся с первой и самой важной частью ARIMA — AR(p), что означает авторегрессию. На деле идея очень проста. 

Авторегрессия — это когда будущее значение ряда предсказывается на основе его же прошлых значений.

Вернемся к нашему кафе. Вы хотите спрогнозировать, сколько посетителей будет в следующем месяце. Логично предположить, что на это число влияет то, сколько гостей было в предыдущие месяцы. Если вы заметили, что после спада в октябре и ноябре следует всплеск в декабре, вы подсознательно используете логику авторегрессии. Модель AR делает то же самое, но на строгом математическом уровне.

Параметр p — это порядок модели, или лаг. Он показывает, насколько далеко в прошлое мы заглядываем, чтобы сделать прогноз.

Если p = 1 (AR(1)), мы предсказываем значение для следующего месяца, используя данные только одного предыдущего месяца. Это как если бы вы говорили: «В декабре к нам придет примерно столько же гостей, сколько в ноябре».

Если p = 3 (AR(3)), модель будет учитывать три предыдущих месяца. Это уже более сложный и, возможно, точный прогноз, который может уловить более длительные циклические паттерны.

Допустим, продажи в кафе за последние три месяца составили 100, 110 и 120 тысяч рублей. Модель AR(3) не просто увидит рост и продолжит линию тренда. Она рассчитает конкретные зависимости: например, насколько сильно значение каждого из этих трех месяцев влияет на будущее. В результате она может дать прогноз, скажем, в 125 тысяч рублей, формально описав выявленную закономерность.

I(d): интегрирование — как сделать ряд стационарным

Перейдем ко второй составляющей — I(d), или интегрированию. В модели ARIMA интегрирование нужно для того, чтобы привести ряд к стационарному виду.

Помните, что ARIMA будет работать корректно лишь в том случае, если данные не имеют ярко выраженного тренда (постоянного роста или падения) или сезонных колебаний и приведены к среднему. I(d) отвечает за это преобразование. 

Параметр d — это порядок дифференцирования. Это число, которое показывает, сколько раз нужно вычесть текущее значение из предыдущего, чтобы привести данные к стационарному виду. Например, если d = 1, значит, нужно вычесть из каждого значения его предыдущее всего один раз, чтобы сделать ряд стационарным.

На практике вы не подбираете d вручную. Вы просто последовательно применяете дифференцирование и после каждого шага проверяете ряд тестом Дики-Фуллера. То значение d, при котором тест наконец-то скажет «ряд стационарен», и будет нашим ответом.

Допустим, сейчас продажи выглядят так (тыс. ₽).

• Исходный ряд (есть тренд): [100, 110, 125, 140, 160] — виден явный рост.
• Применяем дифференцирование (d=1).
  Мы вычисляем не абсолютные значения, а их изменения от месяца к месяцу:
  • 110 — 100 = 10
  • 125 — 110 = 15
  • 140 — 125 = 15
  • 160 — 140 = 20
• Новый, стационарный ряд (изменения): [10, 15, 15, 20]

Мы убрали общий тренд на рост. Теперь мы анализируем не сами продажи, а ежемесячный прирост. Этот новый ряд уже гораздо ближе к стационарному: он колеблется вокруг среднего значения прироста (около 15), и именно с ним будет работать ARIMA.

MA(q): модель скользящего среднего — учитываем ошибки прошлых прогнозов

Перейдем к последнему компоненту — MA(q), что означает скользящее среднее. Если AR смотрела на сами прошлые значения, то модель MA обращает внимание на неожиданные всплески или провалы, которые уже произошли.

Представьте, что ваша AR-модель спрогнозировала для кафе 100 посетителей в понедельник. Но в тот день неожиданно разразилась гроза, и пришло всего 70 человек. Разница в 30 человек — это и есть та самая «ошибка» или, точнее, непредсказуемое событие (шок).

Модель MA(q) исходит из простой идеи: неожиданные события часто имеют краткосрочные последствия. Если вчера был ливень, который отпугнул клиентов, то часть из них может прийти сегодня. MA-модель пытается уловить этот эффект.

Параметр q показывает, насколько далеко в прошлое мы заглядываем, чтобы учесть эти случайные шоки.

Если q = 1 (MA(1)), модель учитывает влияние вчерашней случайности на сегодняшний прогноз.

Если q = 2 (MA(2)), она учитывает влияние вчерашней и позавчерашней неожиданностей.

Допустим, в понедельник произошел тот самый провал на 30 человек. Во вторник погода наладилась. Модель MA(1) может дать прогноз на вторник не только на основе обычной посещаемости по вторникам, но с поправкой: «Раз в понедельник был негативный шок, часть отложенного спроса реализуется сегодня. Добавим к базовому прогнозу, скажем, 15 человек».

Таким образом, модель учитывает последействия прошлых случайных событий для того, чтобы сделать текущий прогноз более точным.

Общая формула ARIMA(p,d,q)

Теперь, когда мы поняли смысл каждого компонента, давайте взглянем на его математическую запись. Это поможет увидеть модель как единое целое.

Общая формула модели ARIMA(p,d,q) для временного ряда yₜ выглядит так:

ϕₚ(B) (1 − B)ᵈ yₜ = θᵩ(B) εₜ

Давайте расшифруем эту формулу по частям, слева направо.

• (1 − B)ᵈ yₜ — компонента I(d). 

B — это оператор сдвига назад, где B yₜ = yₜ₋₁ (значение ряда в момент t-1). Выражение (1 − B) — это одна операция дифференцирования, т.е. мы вычитаем вчерашнее значение из сегодняшнего. Степень d показывает, сколько раз мы применяем эту операцию, чтобы получить стационарный ряд.

• ϕₚ(B) — компонента AR(p).

Это многочлен: ϕₚ(B) = 1 − ϕ₁B − ϕ₂B² − … − ϕₚBᵖ
Коэффициенты ϕ₁, ϕ₂, … ϕₚ — это веса, которые модель обучается находить. Они показывают, насколько сильно каждое из последних p-значений (yₜ₋₁, yₜ₋₂, …, yₜ₋ₚ) влияет на текущее значение yₜ.

• θᵩ(B) — компонента MA(q). 

Это многочлен: θᵩ(B) = 1 + θ₁B + θ₂B² + … + θᵩBᵩ
Коэффициенты θ₁, θ₂, … θᵩ — это веса для прошлых ошибок прогноза. Они показывают, насколько сильно каждое из последних q случайных возмущений (εₜ₋₁, εₜ₋₂, …, εₜ₋ᵩ) влияет на текущее значение yₜ.

• εₜ — это белый шум. 

Представляет собой случайную, непредсказуемую ошибку в момент времени t. То, что остается после того, как мы учли все закономерности (AR и MA).

В итоге, эта формула — компактное представление всего того, о чем мы говорили: мы стабилизируем данные (I), находим в них внутренние закономерности (AR) и учитываем влияние недавних случайных событий (MA), чтобы сделать наилучшее возможное предсказание.

Пошаговый алгоритм построения модели ARIMA

Подробно разберем ключевые шаги, которые помогут вам создать и настроить свою статистическую модель: от подготовки данных до оценки качества прогноза.

Шаг 1. Подготовка данных и визуализация временного ряда

Прогнозирование не прощает небрежности: как говорится, «мусор на входе — мусор на выходе». Главное на этом этапе — убедиться, что данные не только собраны, но и правильно оформлены.

Что сделать?

• Проверить хронологический порядок. Данные должны быть отсортированы по времени, от старых к новым.
• Обеспечить постоянную частоту. Все наблюдения должны быть сделаны через равные промежутки времени. Например, только по дням, только по месяцам или только по годам. Смешивание разных интервалов в одном ряду недопустимо.
• Обработать пропуски. Если нет информации за какой-то период, такие пробелы нельзя игнорировать. Нужно либо удалить эти строки, либо заполнить пропуски. Например, с помощью интерполяции или скользящего среднего.
• Разобраться с выбросами. Резкие, аномальные скачки могут быть как ошибкой измерения, так и реальным событием. Важно понять их природу и при необходимости сгладить, чтобы они не исказили модель.

Самый простой способ визуализировать подготовленные данные — построить линейный график. В библиотеке matplotlib для Python это можно сделать с помощью одной команды:

Один взгляд на график может дать больше информации, чем десятки статистических тестов. Но на что смотреть?

• Тренд. Есть ли очевидный рост или падение данных с течением времени? Например, если продажи вашего кафе постепенно растут, это будет видно.

• Сезонность. Повторяются ли определенные колебания в течение определенных периодов (например, больше клиентов летом, меньше зимой)?

• Выбросы. Есть ли значения, которые сильно отличаются от других? Например, если в один месяц продажи резко упали, это может быть выбросом.

Визуализация поможет понять, нужно ли корректировать данные.

Шаг 2. Проверка на стационарность и преобразование ряда (дифференцирование)

Один из самых распространенных способов проверить, является ли ряд стационарным, — тест Дики-Фуллера (ADF-тест), который уже упоминали. Он проверяет, имеет ли ряд тренд или другие нестационарные компоненты.

В Python это легко сделать с помощью функции adfuller из библиотеки statsmodels:

Если данные не стационарны, их нужно преобразовать. Один из самых простых способов это сделать — дифференцирование, т.е. мы вычитаем из текущего значения предыдущее. 

Например, если у вас есть данные о продажах, и они растут с каждым месяцем, то дифференцирование будет выглядеть так:

• Месяц 1: 100
• Месяц 2: 110
• Месяц 3: 120

После дифференцирования:

• Разница между месяцем 1 и месяцем 2: 110 — 100 = 10
• Разница между месяцем 2 и месяцем 3: 120 — 110 = 10

Так мы получаем данные, которые показывают только изменения — дифференцированные значения.

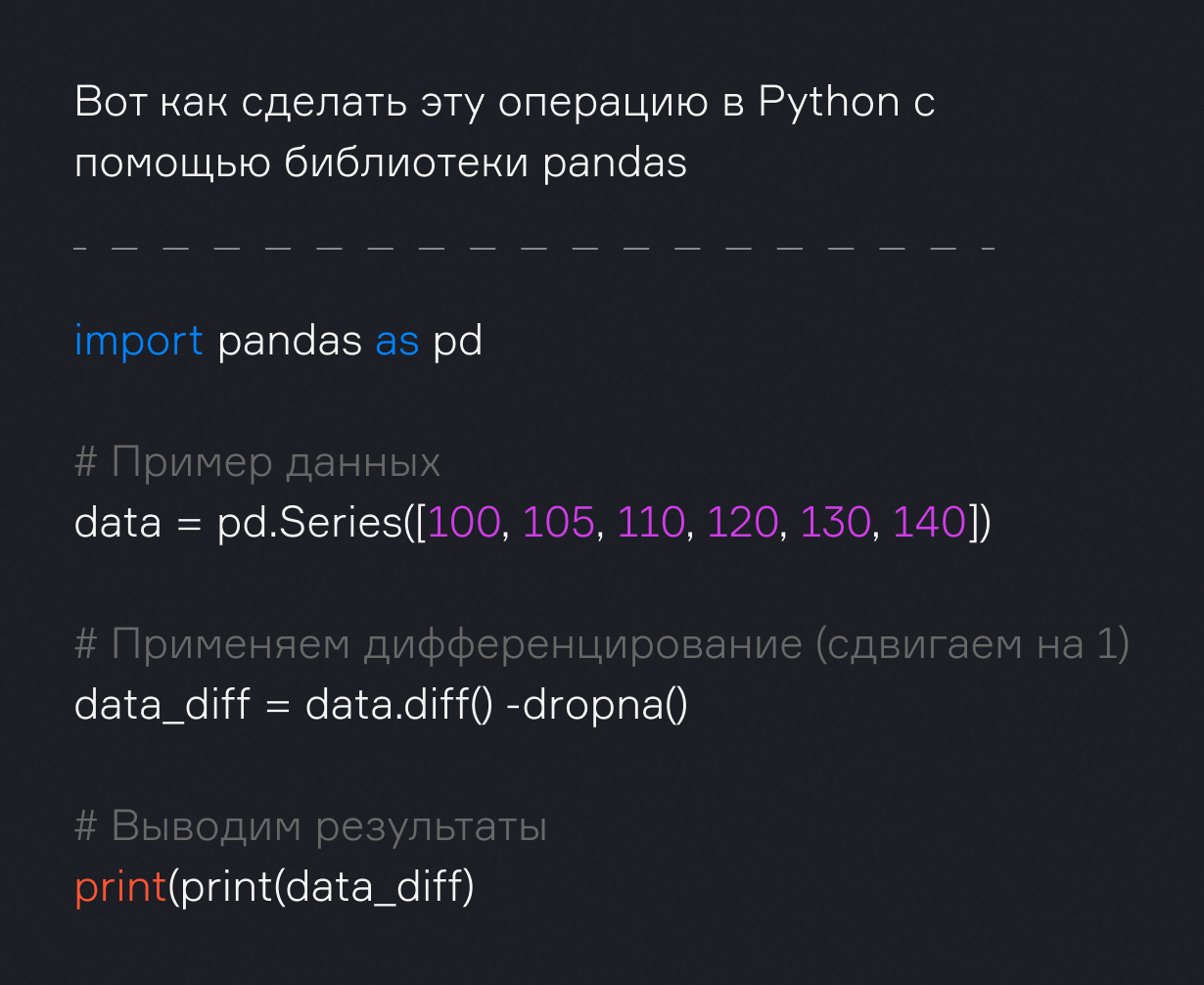
Важно

После дифференцирования нужно снова проверить данные на стационарность с помощью теста ADF. Если ряд не стационарен, все повторить.

Шаг 3. Подбор параметров (p, d, q) с помощью ACF и PACF графиков

ACF (автокорреляционная функция) показывает, как значения временного ряда соотносятся с его предыдущими значениями. Помогает понять, есть ли зависимость между текущим значением и предыдущими значениями ряда.

PACF (частичная автокорреляционная функция) помогает выявить корреляцию между текущим значением и предыдущими значениями, исключая влияние промежуточных значений. Это нужно, чтобы точнее понять, сколько именно предыдущих значений важно учитывать для прогноза.

Сравните.

• ACF: «Сегодня в кафе много посетителей, потому что была хорошая погода последние несколько дней» (учет общей картины).
• PACF: «Сегодня в кафе много посетителей, потому что именно в этот день недели всегда много людей» (учет прямого влияния конкретного дня, а не предыдущих).

ACF помогает подобрать параметр d и q для MA-модели.

PACF помогает подобрать параметр p для AR-модели.

Шаг 4. Обучение модели и анализ ее качества (AIC/BIC критерии)

Когда мы определили параметры, можно приступить к обучению модели. В Python для этого используется класс ARIMA из библиотеки statsmodels. В результате выполнения кода модель обучится, и мы сможем оценить ее параметры, включая коэффициенты, стандартные ошибки и т.д.

Критерии AIC (Akaike Information Criterion) и BIC (Bayesian Information Criterion) используют, чтобы оценить качество модели. Принцип прост:

Чем МЕНЬШЕ значение AIC или BIC, тем ЛУЧШЕ модель.

Эти метрики оценивают, насколько:

• хорошо модель описывает ваши исторические данные;
• модель сложная (чем больше параметров p и q, тем сложнее).

Слишком сложная модель — враг хорошего прогноза. Она начнет подстраиваться под случайный шум в данных, что называется переобучением. На выходе будет идеально предсказывать прошлое, но очень плохо — будущее.

В работе с данными главное — не просто знать алгоритмы, а уметь решать практические задачи. Такой подход предлагает «Симулятор Data Science». Здесь вы сможете сразу закрепить новые знания: построить прогнозы для реальных данных из разных индустрий, развернуть модели и интегрировать их в работающие системы. Это не просто курс, а практическая среда, где вы прокачаете навыки через решение бизнес-задач разной сложности.

Практический пример: строим прогноз продаж на Python

От теории к практике. Представим, что у нас есть данные о ежемесячных продажах кофе в нашем кафе за последние несколько лет. Нужно спрогнозировать, сколько чашек кофе мы продадим в следующем квартале. Сделаем это с помощью Python — главного инструмента современных аналитиков.

Загрузка данных и библиотек 

Для начала подключаем библиотеки, которые помогут нам выполнить всю работу.

• pandas поможет нам загрузить и обработать данные.
• matplotlib нарисует наглядные графики.
• statsmodels — наша главная библиотека для построения моделей, включая ARIMA.

Теперь загрузим данные о продажах, предполагая, что они хранятся в CSV-файле с колонками Date и Sales.

Визуальный анализ и проверка стационарности

Прежде чем строить модель, важно понять структуру данных. Самый простой способ — построить график.

При анализе графика спрашиваем себя:

• Есть ли тренд? Растут ли продажи со временем?
• Видна ли сезонность? Например, заметны ли всплески каждое лето?

Теперь проверим, стационарен ли ряд, с помощью теста Дики-Фуллера.

Если p-value > 0.05, то ряд не стационарен. Применим дифференцирование для получения стационарного ряда, установив параметр d=1.

Подбираем параметры для нашей задачи

Чтобы построить модель ARIMA, нужно выбрать три ключевых параметра: p, d и q.

• d мы уже выяснили на предыдущем шаге. Это количество дифференцирований, которое мы применили к ряду (в данном случае 1).
• p и q подберем с помощью графиков ACF и PACF.

На PACF ищем точку, где столбики впервые резко обрываются за пределами синей области. Этот лаг будет нашим кандидатом для p. На ACF ищем аналогичную точку резкого обрыва для q.

Если это выглядит сложным, тренируйтесь на простых значениях p=1, d=1, q=1.

Обучаем модель ARIMA и визуализируем прогноз

Пришло время создать и обучить модель с выбранными параметрами. В нашем случае это будет ARIMA(1, 1, 1).

В сводке модели обратите внимание на столбец P>|z|, т.е. p-value для коэффициентов. Хорошо, если эти значения меньше 0.05. Значит, коэффициенты значимы. Сделаем прогноз на 12 месяцев вперед и визуализируем его.

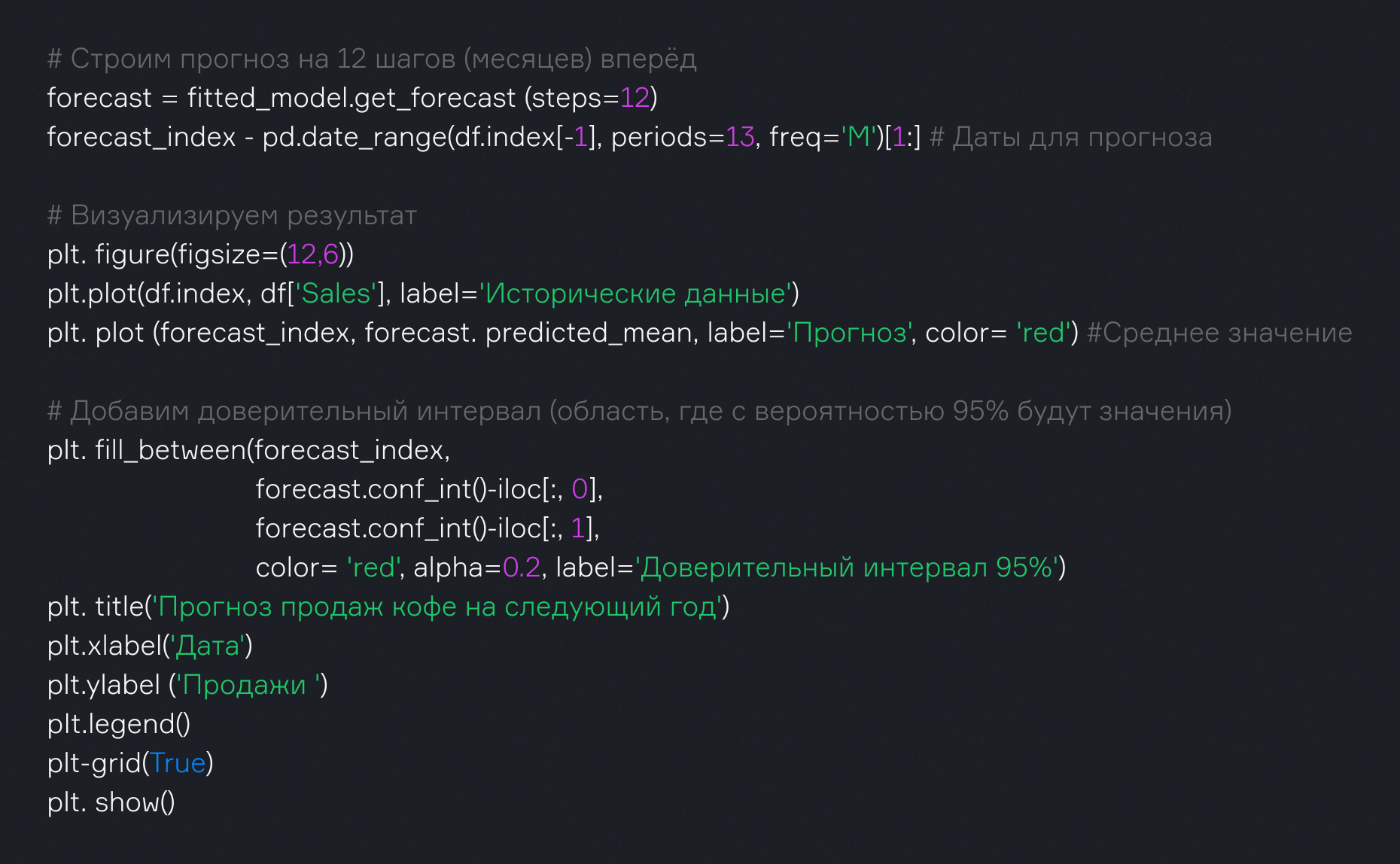
Мы построили прогноз с доверительным интервалом, который показывает все возможные сценарии. Теперь можно уверенно планировать закупки зерен, зная, сколько чашек кофе, скорее всего, будет продано в ближайшие месяцы!

Совет 

Экспериментируйте с параметрами p, d, q и сравнивайте модели по AIC-критерию (чем он меньше, тем лучше), чтобы найти самую точную для ваших данных.

Сравнение ARIMA с другими моделями: SARIMA, ARIMAX

Классическая ARIMA — мощный инструмент, но у реального мира есть свои нюансы. Что делать, если на ваши данные сильно влияет время года? Или если на показатель влияют не только его прошлые значения, но и внешние факторы, например, цена? В таких случаях используют более сложные и специализированные инструменты.

SARIMA: как учесть сезонность в данных

Вернемся к нашему кафе. Допустим, мы построили ARIMA-модель, но она постоянно ошибается в прогнозах на декабрь и летние месяцы. Почему? Потому что мы не учли сезонность. Летом растут продажи айс-кофе, зимой — классического эспрессо.

На помощь приходит SARIMA (Seasonal ARIMA). Та же модель, но с надстройкой для работы с сезонными паттернами.

Представьте, что у вас внутри одного большого тренда (года) есть маленький повторяющийся тренд (месяцы). SARIMA учитывает и то, и другое. У модели появляются дополнительные сезонные параметры.

• P, D, Q — аналоги p, d, q, но для сезонного компонента.
• m — период сезонности. Например, m=12 для месячных данных с годовой сезонностью.

Если вы видите, что продажи кофе в вашем кафе всегда растут в июле, SARIMA это запомнит и автоматически заложит аналогичный рост в прогноз на следующий июль.

ARIMAX: когда нужны дополнительные внешние факторы

Допустим, отдел маркетинга запустил акцию «Вторая чашка кофе со скидкой 50%», и продажи резко выросли. Ни одна ARIMA-модель не сможет предсказать такой скачок, потому что она смотрит только внутрь данных о продажах и не знает о внешних событиях.

Нужна ARIMAX — ARIMA with eXogenous variables. В эту модель мы можем добавить внешние факторы (регрессоры), которые влияют на наш показатель. Какие?

• Экономические: уровень инфляции, курс валют.
• Маркетинговые: бюджет на рекламу, наличие акций.
• Погодные: средняя температура воздуха, количество солнечных дней.
• Календарные: является день праздником или выходным.

Модель по-прежнему учитывает прошлые значения ряда (AR) и прошлые ошибки (MA), но дополнительно учится, как именно каждый внешний фактор влияет на продажи. Формула становится сложнее, но и прогноз — точнее.

Например, вы можете сказать модели ARIMAX: «Сегодня температура на улице +30 градусов, и мы запустили рекламу в соцсетях». Модель учтет это и исторические данные, и даст более обоснованный прогноз на сегодняшний день.

Сильные и слабые стороны ARIMA

Заключение

Не бойтесь экспериментировать! Начните с простых данных, постройте первую модель, проанализируйте ошибки — и вы получите мощный и элегантный способ принимать обоснованные бизнес-решения.