Математический анализ для аналитиков: от пределов до анализа данных простыми словами
Матанализ часто воспринимают как абстрактную теорию из университетских курсов. Но для аналитика это язык, на котором описываются метрики, модели, тренды и процессы. Понимание пределов, производных и интегралов помогает точнее интерпретировать данные, находить закономерности, оценивать рост и принимать решения на основе реальных изменений, а не интуиции.
Содержание
В статье мы разберем этот раздел математики на начальном уровне и покажем, как он работает в задачах аналитики.

Что такое математический анализ и зачем он аналитику данных
Представьте, что хотите понять, как изменится выручка, если повысить цену всего на 1%. Интуитивно кажется, что чуть вырастет. Но на практике все сложнее: спрос может просесть, метрики меняются нелинейно, и где-то там есть точка, после которой рост цены уже не выгоден.
Чтобы найти этот оптимум, мало просто сравнивать до и после. Нужно понять, как именно меняется функция выручки при любом изменении цены. По сути — измерить скорость роста или падения показателя.
Математический анализ — это раздел математики, который изучает, как ведут себя функции: как они меняются, к чему стремятся и как накапливают эффект. Проще говоря, это набор инструментов для отслеживания динамики — роста, спадов, скачков, трендов и накоплений. Именно эти процессы стоят за метриками, моделями и реальными данными.

Основные понятия матанализа на реальных примерах из аналитики
Когда речь заходит об этой теме, большинство людей сразу представляют сложные формулы. Но в аналитике важны не сами формулы, а смысл.
Функции, пределы, производные и интегралы — это не академические термины, а вполне рабочие инструменты, которые помогают понять, почему метрика ведет себя так, как ведет, и что с этим делать.
Эти концепции встречаются практически везде:
- в росте трафика,
- в реакциях пользователей на изменения цены,
- в поведении функции потерь в машинном обучении,
- в A/B-тестах и прогнозах.
Чтобы увидеть в данных живой процесс с динамикой, достаточно освоить несколько базовых идей.
Функция в матанализе
Вся суть аналитической математики заключается в простой идее — понять, как одно влияет на другое. Ключевым инструментом для этого является функция, самая базовая модель в математическом анализе.
Представьте функцию как аккуратный способ описать связь между двумя величинами. Например:
- как растут продажи, если увеличивать бюджет на рекламу;
- как меняется удержание пользователей при улучшении онбординга;
- как растет загрузка сервера при росте числа запросов.
В каждом из этих случаев функция позволяет сформулировать: «Если Х меняется вот так, то Y отреагирует вот так».
f:X→Y
Всё вокруг — функции: зависимость цены дома от его площади, вероятность оттока клиента от его активности, спрос на товар от сезона. График — это визуальное представление этой зависимости. Умение читать графики (определять тренды, выбросы, периодичность) — один из ключевых навыков аналитика.

Предел: предсказание поведения
Иногда процессы развиваются неравномерно: рост замедляется, показатели стабилизируются или вовсе перестают меняться. Здесь вводится понятие предела. Это инструмент, который помогает понять, к чему в итоге стремится метрика, даже если она еще не дошла до пикового значения.
Представьте, что работаете над повышением конверсии при регистрации. Выкатываете новую фичу на сайт, проводите эксперименты, оптимизируете каждый шаг воронки. Конверсия растет, но все медленнее. Было 4.1%, потом 4.4%, затем 4.55%, 4.6% — приросты все меньше и меньше.
Спрашивается, а какое максимальное значение конверсии вообще возможно?
Это и есть тот случай, когда нужен предел.
Предел помогает ответить:
- К какому значению стремится метрика при бесконечном улучшении?
- Есть ли потолок, после которого дальнейшие усилия почти ничего не дадут?
- Как будет вести себя функция, когда значения очень большие или когда переменная приближается к определенной точке?
Это способ спрогнозировать поведение системы, не дожидаясь, пока она реально дойдет до конечного состояния.
Производная: скорость изменения и экстремумы
Если функция описывает зависимость между двумя величинами, то производная показывает, насколько быстро эта величина меняется в каждой точке.

Например, вы наблюдаете рост продаж после запуска рекламной кампании. Сначала продажи растут стремительно, потом рост замедляется и наконец стабилизируется. Производная помогает измерить эту скорость: на каком этапе изменения идут быстрее всего, а где почти останавливаются.
Кроме того, производная помогает находить экстремумы — точки, где функция достигает максимума или минимума. В аналитике это особенно важно, когда нужно понять, где находится оптимум:
- оптимальная цена продукта, при которой выручка максимальна;
- количество показов рекламы, при котором ROI наибольший;
- нагрузка на сервер, после которой начинаются сбои.
Производная позволяет понять не только текущее положение, но и направление движения.
Интеграл: суммирование и накопленный эффект
Если производная показывает скорость изменений, то интеграл позволяет понять, сколько всего накопилось за определенный промежуток. Другими словами, это инструмент суммирования и оценки общего эффекта.
Допустим, вы ежедневно анализируете трафик на сайте. Отдельные дни могут колебаться: в понедельник было 1000 посетителей, во вторник — 1200, а в среду — 950. Интеграл позволяет подсчитать общее количество посетителей за неделю, месяц или квартал, учитывая все колебания.
С его помощью можно оценивать накопленный эффект изменений. Например:
- сколько суммарной выручки принесла новая акция за месяц;
- сколько пользователей привлекла маркетинговая кампания за квартал;
- какая общая нагрузка на сервер за время пикового периода.
Проще говоря, если производная показывает, как быстро что-то меняется, то интеграл — сколько всего накопилось. Вместе эти два инструмента дают аналитикам более полную картину.
Матанализ в работе аналитика: 3 ключевые области применения
Понимание производных, интегралов и пределов помогает видеть закономерности, находить оптимумы и прогнозировать результаты. Далее расскажем, как эти инструменты применяются в ML, анализе трендов и прогнозировании, а также при A/B-тестах и статистических выводах.
Машинное обучение и оптимизация
Если вы когда-либо работали с ML-моделями, то уже сталкивались с математическим анализом, даже не подозревая об этом. Каждый раз, когда алгоритм учится на данных и подбирает оптимальные параметры, в дело вступают производные, частные производные и градиенты.

Градиентный спуск — основной метод оптимизации почти всех современных моделей. Он помогает понять, в какую сторону и насколько изменить параметры модели, чтобы минимизировать ошибку предсказания. Производные показывают скорость изменения ошибки относительно каждого параметра, а градиенты — направление, куда стоит двигаться. Без этих инструментов невозможно корректно обучить модель и достичь хороших результатов.
Матанализ в ML также помогает отслеживать проблемы: слишком резкие шаги могут привести к нестабильному обучению, а маленькие — к медленному прогрессу. Знание основ математического анализа дает ключ к пониманию того, почему модель обучается так, как обучается, и как сделать этот процесс эффективнее.
Анализ временных рядов и прогнозирование
Допустим, вы аналитик в компании, которая продаёт сезонные товары, например, зимние куртки. У вас есть данные о продажах за прошлые годы, и вы хотите спрогнозировать спрос на следующий месяц.
Для этого вы строите временной ряд и декомпозируете его на основные компоненты:
- общий рост или спад продаж (тренд),
- повторяющиеся колебания, связанные с холодной погодой (сезонность),
- случайные факторы (шум).
Затем, используя модель ARIMA, строите прогноз. Эта модель учитывает прошлые значения продаж, а также тренд и сезонность. Важным этапом подготовки данных для ARIMA является дифференцирование ряда, которое помогает оценить скорость изменения спроса от периода к периоду и сделать ряд стационарным.
В результате вы получаете прогноз спроса, который помогает компании оптимизировать закупки, планировать маркетинговые кампании и избегать дефицита или излишков на складах.
Математический анализ предоставляет инструменты для понимания динамики показателей во времени. Дифференцирование помогает оценить скорость изменения трендов, а интегрирование используется для суммирования эффектов и вычисления накопленных значений. Эти и другие методы лежат в основе популярных моделей для работы со временными рядами, таких как AR, MA, ARMA и ARIMA.
A/B-тестирование и статистические выводы
В работе аналитика A/B-тесты — способ понять, какие изменения реально улучшают показатели. Математический анализ здесь помогает проверять гипотезы и оценивать, насколько различия между группами случайны или статистически значимы.
Аналитик формулирует нулевую гипотезу («изменение не влияет на результат») и альтернативную («изменение даёт эффект») и использует статистические тесты. Производные, интегралы и другие методы помогают вычислять z-score, p-value и плотности распределений, чтобы понять вероятность случайного характера наблюдаемых различий.
Например, если p-value очень малая, можно уверенно сказать, что эффект реальный, а не случайный. Интегралы помогают суммировать вероятность по всему диапазону значений, а статистические тесты, такие как t-тест или критерий Манна-Уитни, дают объективную оценку разницы между группами.
Математический анализ также помогает определить, когда можно закончить эксперимент, опираясь на заранее выбранные критерии статистической значимости.
Если хотите прокачать навыки A/B-тестирования в безопасной среде, записывайтесь на курс «Симулятор A/B-тестов». О том, как он устроен, вы узнаете из этого видео:
Матанализ и Data Science: карта изучения
- Начните с основ: функции → пределы → производная.
- Перейдите к ядру DS: частные производные → градиент → понимание градиентного спуска.
- Закрепите связь со статистикой: интегралы → понимание непрерывных распределений.
- Углубитесь для сложных задач: выпуклость → методы оптимизации.
Совет
Не застревайте в теории. Изучая каждую тему, сразу же ищите ей применение: «Как эта производная используется в коде линейной регрессии?» или «Как этот интеграл связан с p-value?». Такой подход превратит абстрактную математику в мощный и понятный инструмент.
Как эффективно изучать матанализ с нуля
Формулы, сложные термины и масштабность темы часто пугают новичков, но разобраться в математическом анализе на базовом уровне реально. Главное — подходить к изучению шаг за шагом и сразу применять знания на практике.
Отличным инструментом для старта является бесплатный курс «Математика для Data Science».
Курс состоит из трёх модулей: два посвящены математическому анализу, а один — линейной алгебре. Каждый урок раскрывает конкретную тему, а внутри урока есть короткие видео, которые объясняют отдельные аспекты темы.

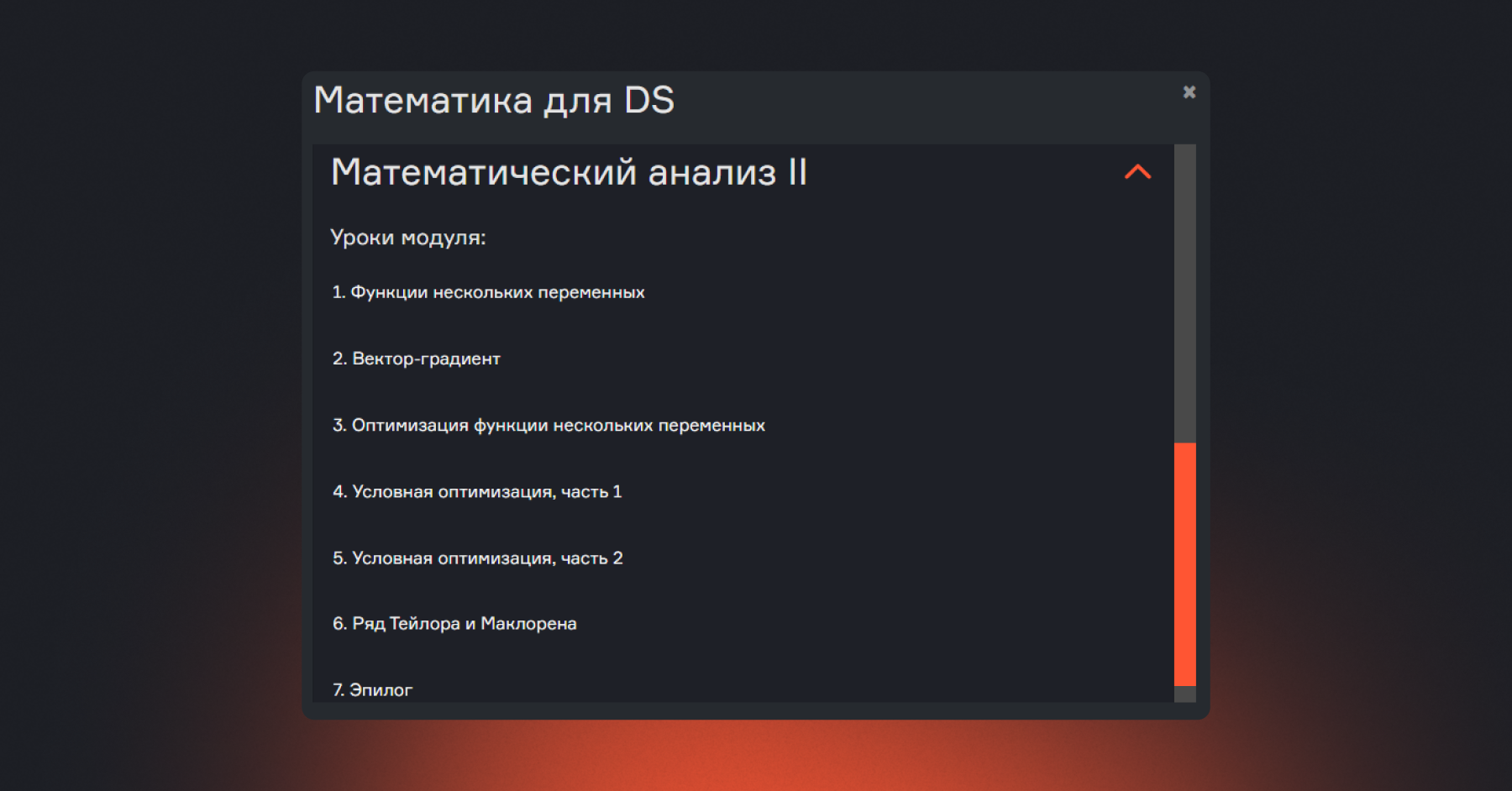
Кроме теории, курс включает практические задания: за выполнение упражнений можно заработать баллы, что помогает закреплять знания и проверять, насколько вы усвоили материал. Такой подход делает обучение пошаговым, понятным и мотивирующим, позволяя уверенно двигаться от базовых концепций к реальным аналитическим задачам.
Заключение
Простыми словами, матанализ — это инструмент, который помогает аналитикам понимать закономерности и принимать обоснованные решения. Мы разобрали основные понятия: функции, пределы, производные и интегралы, а также показали, как они применяются в машинном обучении, прогнозировании и A/B-тестах.
Начните с базовых концепций, используйте практические примеры и онлайн-курсы — и вы убедитесь, что эта область знаний становится понятной и интересной.
