Корреляция в статистике и анализе данных: как провести анализ и правильно интерпретировать результаты
Мы постоянно ищем связи в данных. Кажется логичным, что больше рекламных расходов ведет к росту продаж, а повышение цены — к снижению спроса. Корреляционный анализ позволяет проверить эти гипотезы, давая им численную оценку. Он показывает, есть ли статистическая связь между двумя показателями и насколько она сильна.
Однако если вы обнаружите, что продажи мороженого и число солнечных дней сильно коррелируют, это не значит, что мороженое вызывает жару. Из статьи вы узнаете, что такое корреляция и как использовать этот инструмент: от расчета и визуализации до правильной интерпретации в бизнес-контексте.
Содержание

От бытовой логики к точным числам
Представьте, что смотрите отчет по продажам и замечаете: в те месяцы, когда растут маркетинговые расходы, выручка тоже чаще всего идет вверх. Интуитивно возникает мысль, что между этими показателями есть зависимость. С таких бытовых наблюдений и начинается работа со статистической связью в аналитике.
Простыми словами, корреляция — это мера статистической зависимости между двумя переменными. Она показывает, есть ли между ними связь и в какую сторону.
Важно
Анализ фиксирует сам факт совместного изменения, но не объясняет, почему так происходит. Он не доказывает, что одно событие вызывает другое.
- Положительная корреляция
Один показатель растет — второй тоже растет. Например, увеличение бюджета на контекстную рекламу → рост числа заявок с сайта.
- Отрицательная корреляция
Один показатель растет — второй падает: рост цены на подписку → снижение уровня удержания клиентов.
- Отсутствие связи
Изменения показателей никак не согласованы. Как, допустим, количество выпитого командой разработки кофе и скорость работы сервера.
Если хотите не просто знать о таких инструментах, а уверенно применять их для решения реальных бизнес-задач, приходите на курс «Аналитик данных». Вы научитесь не только строить графики, но и превращать цифры в конкретные рекомендации для роста выручки, удержания клиентов и оптимизации процессов.
Виды коэффициентов корреляции: как выбрать нужный
Для количественной оценки силы и направления связи используют коэффициент корреляции — это число от -1 до 1, которое суммирует выявленную взаимосвязь в одно понятное значение.
- Знак (+ или -) показывает направление связи (прямая или обратная).
- Абсолютное значение (от 0 до 1) показывает силу связи: чем ближе к 1, тем связь устойчивее.
Но как получить это число? Перед расчетами стоит понять, какую именно связь вы ищете и с какими данными работаете.
Таблица-определитель: от ваших данных к правильному методу
На практике аналитик редко начинает с формул. Гораздо важнее сначала ответить на несколько простых вопросов о данных: какие у вас показатели, как они измеряются и какую связь вы хотите проверить. Именно от этого зависит, какой коэффициент корреляции даст корректный результат.
Проще всего представить выбор в виде небольшой таблицы-определителя. Она помогает быстро сопоставить тип данных и подходящий метод корреляции — без углубления в статистическую теорию.
| Коэффициент | Суть вопроса | Тип данных | Пример |
| Пирсона (r) | Насколько хорошо связь описывается прямой линией? | Два непрерывных числовых показателя (бюджет, доход), распределение близко к нормальному. | Оценить, насколько предсказуемо увеличение выручки от роста затрат на performance-маркетинг.
Данные: точные суммы в рублях за каждый месяц. |
| Спирмена (ρ) | Насколько стабилен порядок: если один показатель растет, растет ли и другой? | Любые числовые или порядковые данные, где важны ранги. Устойчив к выбросам. | Понять, связан ли рейтинг приложения с местом в поисковой выдаче.
Данные: ранги, а не абсолютные значения. |
| V Крамера | Есть ли зависимость между категориями в разных группах? | Два категориальных (номинальных) признака. | Выяснить, влияет ли регион пользователя на выбор тарифа в приложении сотового оператора.
Данные: названия категорий. |
Такой подход особенно полезен в бизнес-задачах, где важно быстро получить корректный ориентир, а не идеальный статистический результат. Корреляция здесь выступает как первый фильтр: она подсказывает, куда смотреть дальше и какие гипотезы имеет смысл проверять более глубокими методами.
Линейная связь: коэффициент корреляции Пирсона
В Data Science и бизнес-аналитике это инструмент первого касания в рамках разведочного анализа (EDA).Он отвечает на вопрос: насколько хорошо связь между двумя числовыми переменными описывается прямой линией?
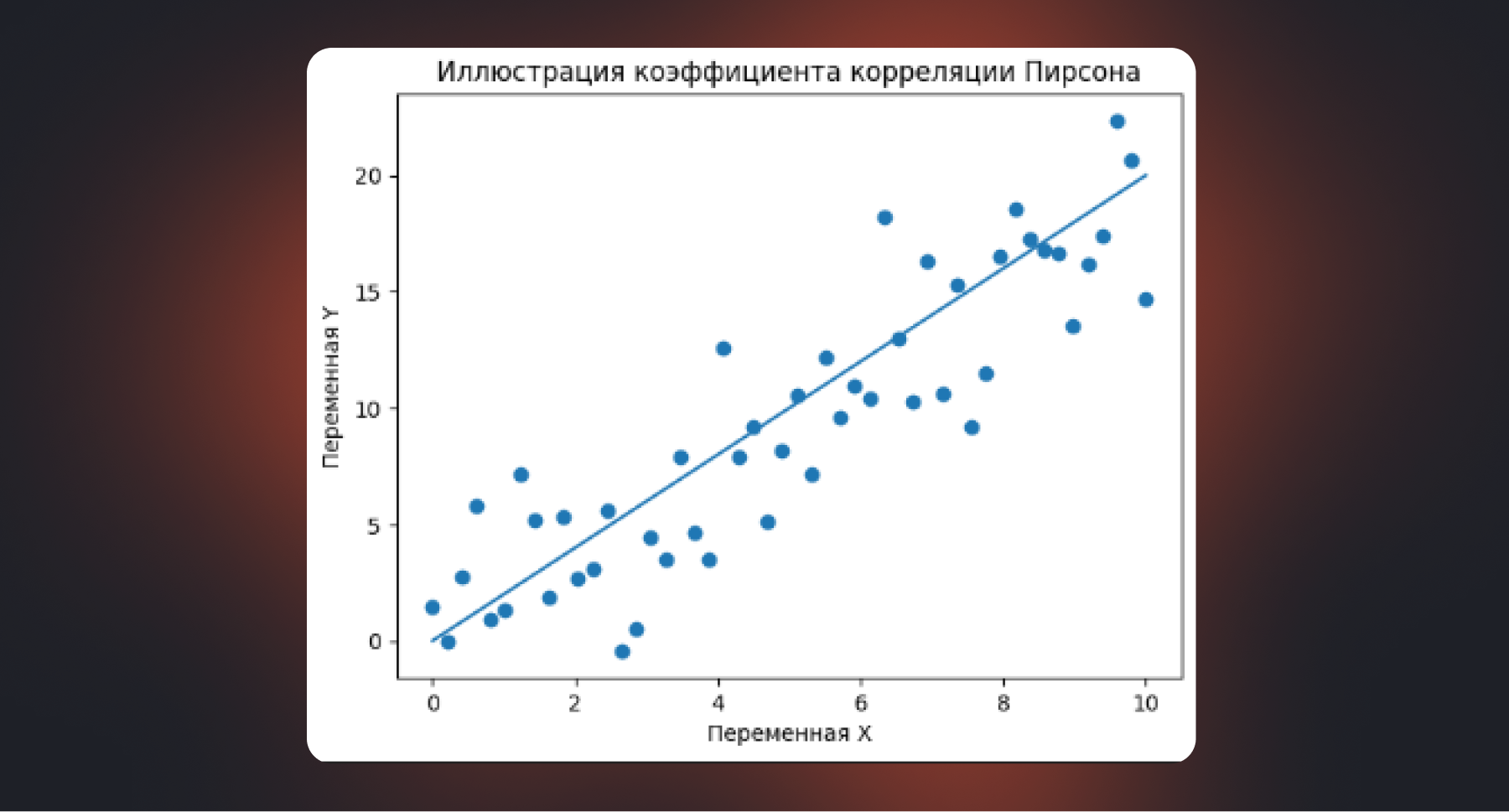
Пирсон хорошо работает, когда оба признака — непрерывные числа и их совместное распределение близко к линейному. Например:
- Маркетинг: бюджет на рекламу vs. количество лидов.
- Продажи: цена товара vs. объем продаж.
- Продукт: время активности пользователя в приложении vs. стоимость его жизненного цикла (LTV).
Значение коэффициента лежит в диапазоне от –1 до +1. Числа, близкие к +1 или –1, говорят о сильной линейной связи, значения около нуля — об ее отсутствии или слабости.
Важно
Пирсон чувствителен к выбросам и плохо отражает нелинейные зависимости. Поэтому в аналитике его стоит использовать осознанно — как быстрый способ проверить гипотезу, а не как окончательное доказательство связи.
Сильный коэффициент — сигнал к тому, чтобы углубиться в анализ: построить линейную регрессию для прогнозирования или тщательно очистить данные от выбросов. Слабый — не означает, что связи нет; это повод поискать ее другими методами (например, Спирменом) или проверить нелинейные модели.
Ранговая связь: коэффициенты Спирмена и Кендалла
Не всегда важно, насколько именно отличаются значения показателей. В ряде задач аналитика больше интересует их порядок: кто выше, кто ниже, кто растет быстрее. В таких случаях говорят о ранговой связи, и здесь на сцену выходят коэффициенты Спирмена и Кендалла.
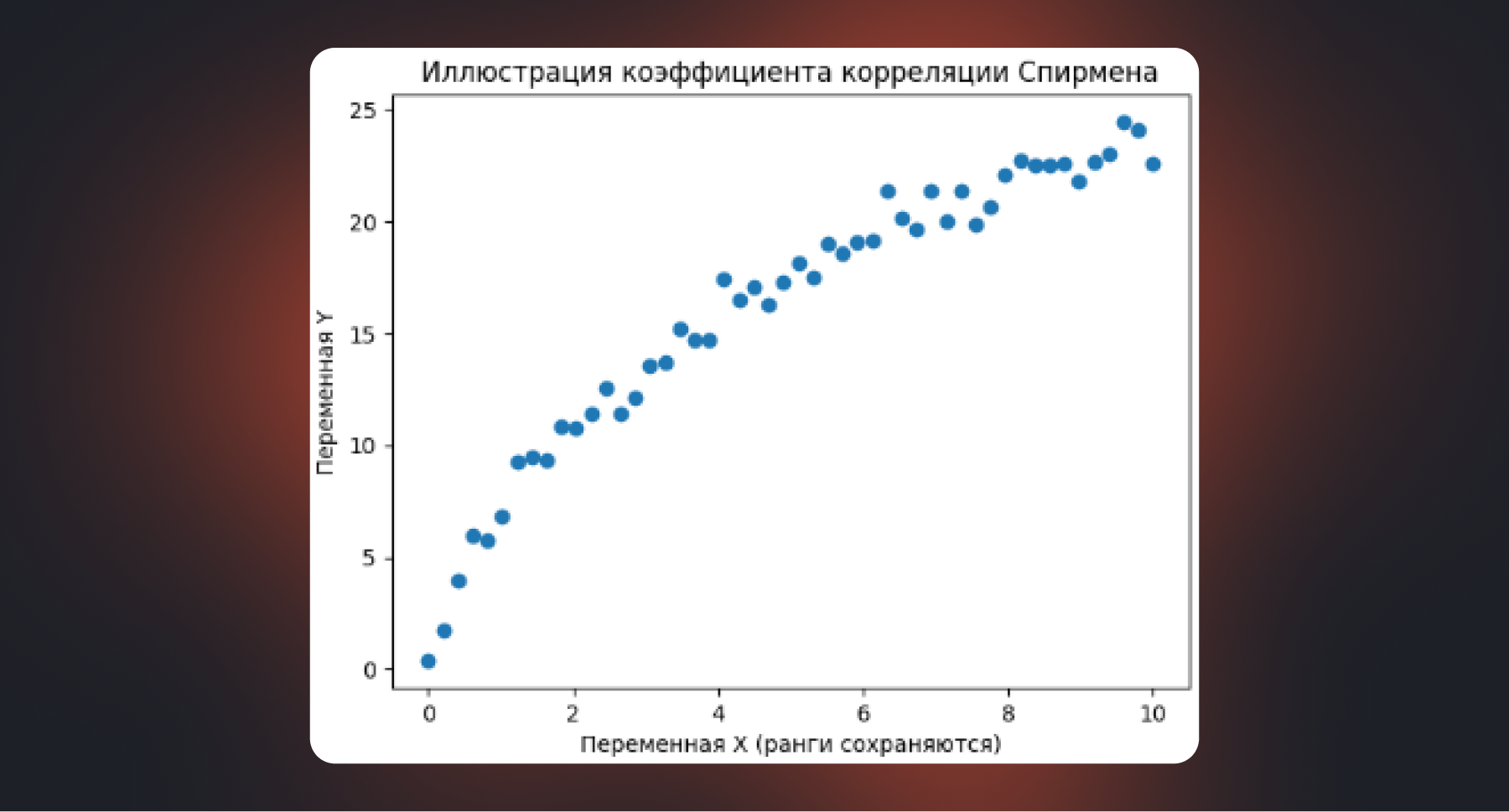
Оба метода работают с рангами, а не с исходными значениями. Проще говоря, данные сначала упорядочиваются, и уже затем оценивается, насколько согласованно меняется этот порядок. Это делает коэффициенты Спирмена и Кендалла более устойчивыми к выбросам и полезными там, где связь есть, но она не обязательно линейная.
В бизнес-аналитике такие коэффициенты часто применяются, например, при анализе рейтингов, оценок пользователей, приоритизации клиентов или сравнении позиций товаров в выдаче. Спирмен используется чаще — он проще в расчете и хорошо подходит для первичного анализа. Кендалл считается более строгим и устойчивым при небольших выборках, но используется реже. В обоих случаях логика та же: это инструмент для выявления возможной зависимости, которая затем требует более детальной проверки.
Для категориальных данных: коэффициент V Крамера
Иногда данные вообще нельзя упорядочить или представить в виде чисел. Например, канал привлечения, регион, тип клиента или категория товара. В таких случаях привычные коэффициенты корреляции не работают — им просто не с чем сравнивать значения. Для анализа связи между категориальными признаками используют коэффициент V Крамера.
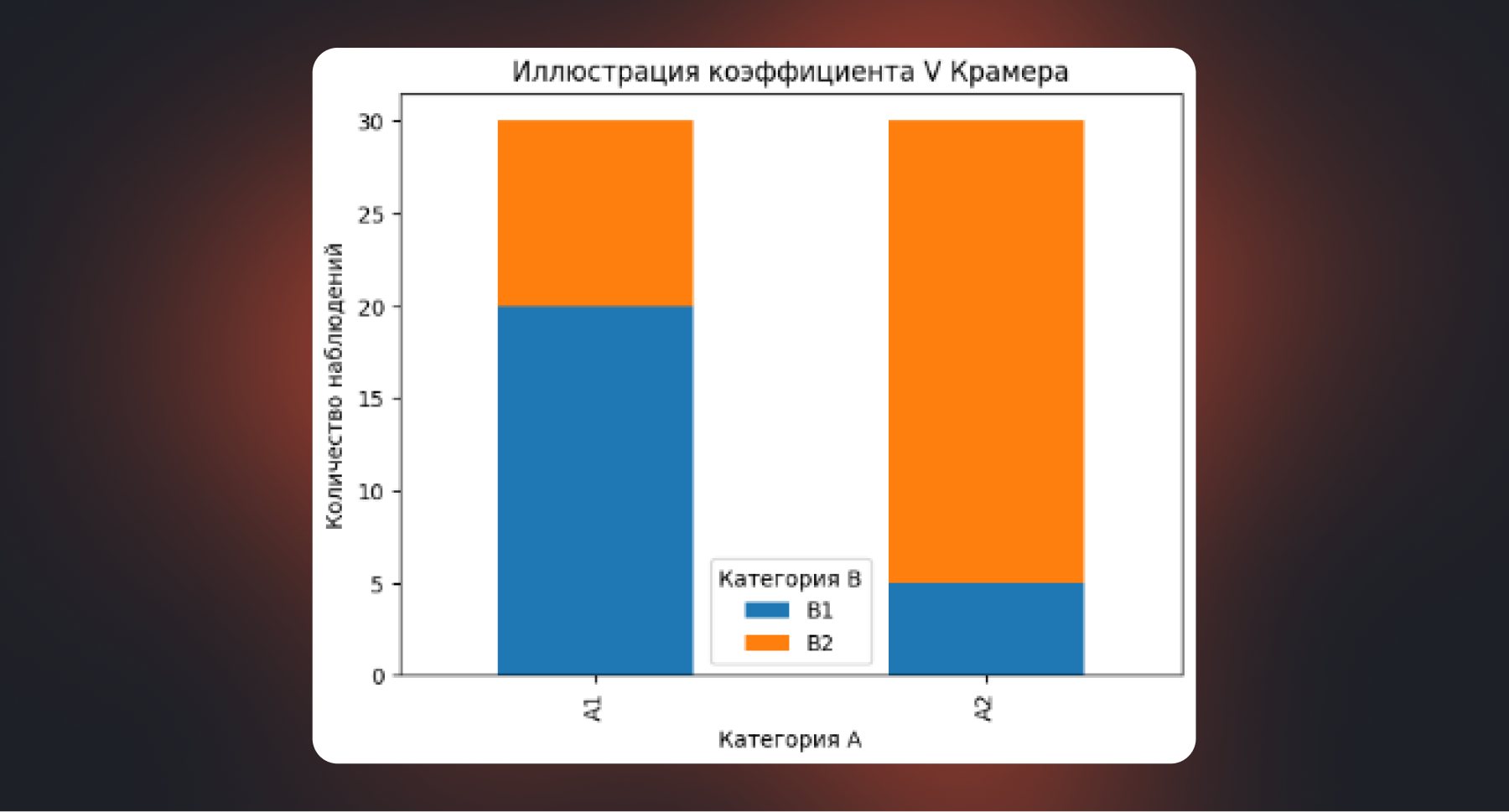
Он отвечает на вопрос: «Насколько распределение одной категории зависит от другой?» Это ваш инструмент для категориального EDA. Он систематизирует то, что вы могли бы интуитивно заметить, изучая доли и проценты в сводных таблицах. Обнаружив умеренную или сильную связь, вы получаете четкий сигнал для:
- Глубокой сегментной аналитики. Например, проанализировать профиль клиентов, выбирающих электронику в рассрочку.
- Принятия продуктовых решений. Допустим, оптимизировать методы оплаты под ключевые категории товаров.
- Построения более точных моделей машинного обучения, корректно учитывающих категориальные признаки.
Значение здесь лежит в диапазоне от 0 до 1. Ноль означает отсутствие связи, значения ближе к единице — более сильную зависимость. Как и любая корреляция, коэффициент V Крамера не объясняет причины. Он лишь дает сигнал, что между признаками есть связь и ее стоит изучить глубже — уже с учетом контекста и бизнес-логики.
Кратко
- Если оба показателя — числа и вы ожидаете примерно прямую зависимость → Пирсон.
- Если важны ранги или данные зашумлены выбросами → Спирмен.
- Если у вас категории → V Крамер.
Пошаговая инструкция: как провести корреляционный анализ
Полезный результат начинается не с формулы, а с правильной последовательности шагов. Ниже — базовый алгоритм, который подходит и для бизнес-аналитики, и для задач Data Science.
Шаг 1. Сформулируйте четкую гипотезу
Хорошая гипотеза — измеримая и конкретная. Например: растут ли продажи вместе с увеличением рекламного бюджета, связана ли частота покупок с возрастом клиента, отличаются ли конверсии в разных каналах.
Это защищает от ложных открытий (p-hacking). Проверяя десятки случайных пар, вы почти гарантированно найдете значимую корреляцию, которая исчезнет на новых данных.
Шаг 2. Визуализируйте данные с помощью диаграммы рассеяния
Перед расчетами полезно просто посмотреть на данные. Диаграмма рассеяния часто дает больше понимания, чем сам коэффициент. Она помогает увидеть форму связи, наличие выбросов и понять, есть ли вообще зависимость.
Например, вы проверяете гипотезу о связи маркетинговых расходов и выручки. На графике видно, что зависимость похожа на логарифмическую кривую, т.е. после определенного порога рост трат дает все меньший прирост. В таких случаях слепой расчет корреляции Пирсона может дать ложный результат.
Шаг 3. Выберите коэффициент по таблице выше
Когда вы понимаете, какие данные у вас есть и как они выглядят, можно выбирать метод.
Этот шаг часто пропускают, но именно он определяет корректность всего анализа. Неправильно выбранный коэффициент может создать иллюзию связи там, где ее нет, или скрыть действительно важную зависимость.
Шаг 4. Рассчитайте значение
Недостаточно получить только коэффициент, т.к. без проверки статистической значимости он легко может оказаться случайным совпадением. Поэтому корректный шаг 4 всегда состоит из двух частей: расчета коэффициента и оценки p-value.
Excel и Google Таблицы
Для базового анализа можно использовать встроенную функцию:

Она считает коэффициент Пирсона и подходит для первичной проверки. Однако Excel и Google Таблицы не показывают p-value автоматически — для этого потребуются дополнительные вычисления или надстройки. Поэтому такие инструменты удобны для быстрого ориентира, но ограничены для более строгого анализа.
Python
В аналитической работе чаще используют Python — он позволяет сразу получить и коэффициент, и статистическую значимость.
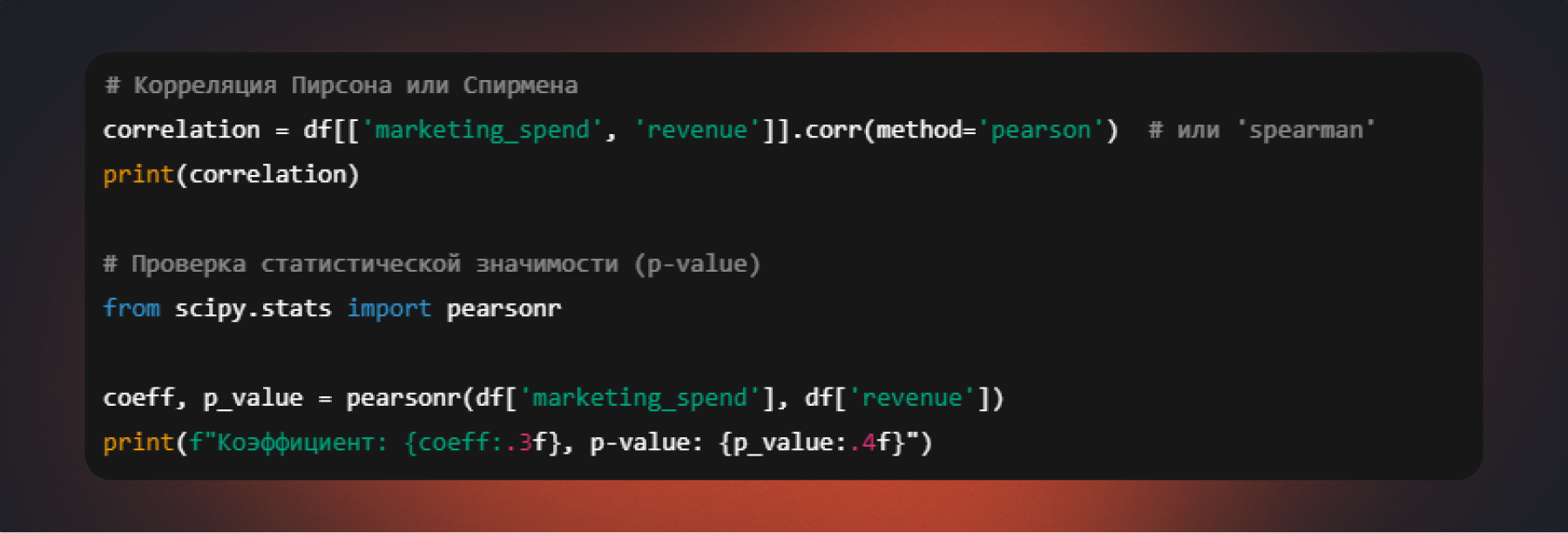
После этого важно интерпретировать коэффициент и p-value вместе, а не по отдельности:
- Коэффициент = 0.75, p-value = 0.001
Сильная и статистически значимая связь. Вероятность случайного совпадения низкая — гипотеза заслуживает дальнейшего анализа.
- Коэффициент = 0.60, p-value = 0.12
Связь выглядит умеренной, но статистически не подтверждена. Высок риск, что наблюдение случайно, — гипотеза не подтверждается.
Важно
Корреляционный анализ — это процесс верификации гипотезы. Его итог — не число в отчете, а обоснованное решение о том, куда направить ресурсы для более глубокого исследования, которое уже может привести к управленческим решениям.
Как интерпретировать результаты: сила связи и главные ловушки
Не стоит сразу делать выводы. Особенно если коэффициент высокий и выглядит убедительно. Хороший иллюстративный пример: количество фильмов с Сильвестром Сталлоне, выходивших в прокат, сильно коррелирует с числом убийств в США, связанных с неправильным использованием зубной нити. За период 2000–2010 годов коэффициент корреляции между этими показателями составляет r = 0,92. На графике видно почти идеальное совпадение динамики. И при этом очевидно, что фильмы Сталлоне никак не вызывают несчастные случаи с зубной нитью.
Это хорошо показывает ключевую ловушку: сильная корреляция не означает причинно-следственную связь. Совпадение может быть случайным, опосредованным третьим фактором или вовсе не иметь практического смысла.
Чек-лист для безопасной интерпретации
Прежде чем делать выводы, спросите себя:
- Значимость: p-value < 0.05?
- Контекст: Есть ли логическое, предметное объяснение связи? Если нет — это красный флаг.
- Скрытые факторы: Мог ли третий, неучтенный показатель влиять на оба?
- Причина и следствие: Мы уверены в направлении влияния? Не может ли оно быть обратным?
- Следующий шаг: Что мы сделаем на основе этого? Запустим A/B-тест, построим регрессию с контрольными переменными, соберем больше данных?
Правильная интерпретация корреляции — это всегда комбинация чисел и здравого смысла. Она должна вести к более глубокому анализу: проверке гипотез, учету дополнительных факторов и поиску реальных причин, а не останавливаться на одном коэффициенте.
Корреляция в работе: практические примеры для аналитиков и маркетологов
Сценарий 1. Оценка эффективности каналов в маркетинге
Задача: определить, какие каналы привлечения стоит масштабировать.
Действие: считаем корреляцию (Пирсона или Спирмена) между ежедневными или еженедельными расходами на канал и количеством целевых действий (лиды, продажи) с учетом лага в 1-7 дней.
Пример результата: сильная положительная корреляция (r > 0.7) для контекстной рекламы и слабая (r < 0.3) для социальных сетей.
Нельзя: сразу перенаправлять весь бюджет в контекстную рекламу.
Нужно: запустить инкрементальный тест (например, гео-эксперимент), чтобы измерить чистый эффект от увеличения бюджета. Или построить регрессионную модель с насыщением, чтобы найти точку, где рост затрат перестает быть эффективным.
Сценарий 2. Отбор признаков для ML-модели
Задача: улучшить прогнозную модель оттока клиентов (churn).
Действие: на этапе разведочного анализа (EDA) строим корреляционную матрицу для всех числовых признаков (частота покупок, сумма чека, время с последнего визита, количество обращений в поддержку) с целевой переменной «Факт оттока».
Пример результата: сильная отрицательная корреляция оттока с частотой покупок и слабая — с суммой чека.
Нельзя: слепо включить в модель все признаки с высокой корреляцией, не проверив на мультиколлинеарность, т.е. сильную корреляцию между самими признаками, например, «Частота» и «Общая сумма».
Нужно: использовать найденные признаки как кандидаты для модели. Перед обучением проверьте, не дублируют ли они друг друга и действительно ли важны для результата.
Сценарий 3. Поиск узких мест для операционной аналитики
Задача: снизить текучку кадров в колл-центре.
Действие: анализируем связь между средней нагрузкой оператора (число обращений на смену) и фактом его увольнения в течение квартала (категории да/нет). Используем коэффициент V Крамера.
Пример результата: обнаружена умеренная ассоциация (V = 0.4).
Нельзя: сразу заявить, что нагрузка — единственная причина увольнений.
Нужно: провести глубокий сегментный анализ: разбить данные по сменам, опыту работы, типу обращений. Затем провести анкетирование, чтобы найти истинные причины (стресс, зарплата, карьера). Это отправная точка для HR-расследования.
Вывод
Корреляция в каждом из этих сценариев заменяет размытое «нам кажется» на конкретное «вот два показателя, которые движутся вместе, и сила их связи равна X».
Заключение
Мы разобрали один из самых простых и доступных инструментов в аналитике данных. Корреляционный анализ помогает быстро навести порядок в показателях, заметить возможные связи и сформулировать первые гипотезы. При этом он не объясняет причины и не дает готовых решений.
Сильная связь в цифрах — повод задать правильные вопросы, а не сделать окончательный вывод. Без учета контекста, бизнес-логики и последующего анализа коэффициенты легко вводят в заблуждение.
