Квадратичная функция: свойства графика параболы и построение с примерами

Мир вокруг редко ведет себя линейно. Продажи растут, потом замедляются. Стоимость рекламной кампании увеличивается, но эффективность начинает падать. Производительность растет до определенного момента, а дальше — наоборот. Во всех этих ситуациях данные ведут себя по параболе. И чем лучше вы это понимаете, тем легче будет читать такие зависимости и принимать решения.

В статье разбираем квадратичную функцию: что это, как построить ее график и как эти знания помогают аналитикам в реальной работе. 

Что такое квадратичная функция: определение и формула

Представьте, что анализируете эффективность рекламных вложений. На первых этапах каждая дополнительная тысяча рублей приносит больше клиентов, но со временем рост замедляется, а затем может даже начать падать. Такую зависимость уже не опишешь прямой линией, ведь она изгибается, формируя плавную дугу.

Квадратичная функция — это одна из базовых математических моделей, которая точно описывает подобные нелинейные зависимости. Она позволяет отображать процессы, где есть ускорение, замедление, оптимальная точка или максимум/минимум. Поэтому квадратичные зависимости встречаются в аналитике гораздо чаще, чем кажется: от реакций пользователей на изменение цены до оценки ROI рекламных каналов.

Общая формула выглядит так:

f(x) = ax² + bx + c

где:

• x — независимая переменная (аргумент),
• a, b, c — коэффициенты, причем a ≠ 0.

Переменную x не нужно искать — ее выбирают, задают по условию задачи или в зависимости от контекста. Это входное значение.

Коэффициенты

a — ключевой коэффициент, который отвечает за форму графика квадратичной функции. Он задает направление ветвей параболы (вверх при a > 0 или вниз при a < 0) и определяет, насколько быстро функция растет или убывает.

b — смещает график влево или вправо и влияет на положение вершины — точки максимума или минимума.

c — значение функции при x = 0. В практических задачах это может быть исходный уровень метрики без влияния факторов. Например, базовый уровень продаж или эффект без инвестиций.

Любая кривая роста, динамика метрик, точка оптимума, реакция пользователей — все это опирается на математику. Чем глубже вы идете в аналитику, тем важнее уверенно знать базу.

Перестать бояться формул поможет бесплатный курс «Математика для Data Science». Он дает опору в ключевых разделах: математическом анализе и линейной алгебре. Вы научитесь уверенно читать формулы, решать простые задачи из высшей математики и применять математическую логику в задачах анализа и ML.

Как выглядит график квадратичной функции

Как уже упоминалось выше, это парабола — симметричная кривая, открытая либо вверх, либо вниз.

У нее всегда есть вершина — точка, где функция достигает экстремума. В аналитике это место, где показатель максимален или минимален: например, оптимальный бюджет, минимальное время отклика или идеальный уровень скидки.

Свойства квадратичной функции: разбор

Поговорим о характеристиках, которые позволяют заранее понять форму и ключевые особенности графика. Для аналитиков эти параметры помогают оценить поведение показателя без необходимости строить полную визуализацию.

Область определения и область значений

У параболы есть одно очень удобное свойство: она работает при любых значениях x. Значит, что область определения квадратичной функции — то есть все допустимые значения аргумента — всегда:

(−∞; +∞)

Можно подставлять в формулу любое число — функция всегда даст результат. 

А вот область значений — это набор чисел, которые могут быть получены. То есть какие значения показателя возможны в принципе. И здесь все зависит от того, в какую сторону развернута парабола.

• Если коэффициент a > 0, парабола открывается вверх.

Тогда у функции есть самая нижняя точка, а дальше значения растут бесконечно.

Область значений: от минимального значения и выше.

• Если a < 0, парабола открывается вниз.

Тогда у функции есть самая верхняя точка, а дальше значения убывают.

Область значений: от минус бесконечности и до максимального значения.

Например:

• когда бюджет увеличивается, конверсия может расти только до определенного уровня — это верхняя граница;
• при уменьшении цены прибыль может снижаться, но есть точка, ниже которой она уже не упадет — нижняя граница;
• производительность системы может иметь максимум, выше которого рост невозможен.

Нули функции (корни) и пересечение графика с осями

Нули функции или корни — это такие значения x, при которых квадратичная функция равна нулю. На графике это точки, где парабола пересекает ось X.

Формально это решение уравнения:

ax² + bx + c = 0

Количество и тип корней определяются по дискриминанту:

 D = b² — 4ac

• Два различных корня (D > 0), значит, парабола пересекает ось X в двух точках.
• Один корень (D = 0), значит, парабола касается оси X только своей вершиной.
• Действительных корней нет (D < 0), значит, пересечений нет, то есть график всегда находится выше или ниже оси.

Этот метод позволяет быстро оценить поведение функции: есть ли точки, где показатель обнуляется, или же он всегда строго положительный или отрицательный.

Представьте, что вы аналитик, изучающий зависимость прибыли от размера рекламного бюджета. 

1. Сначала с ростом бюджета прибыль увеличивается.
2. Затем эффект от дополнительных вложений снижается, и прибыль достигает максимума.
3. После определенной точки перерасход средств приводит к убыткам.

Как найти нули квадратичной функции в данном случае? Это размеры бюджета, при которых прибыль равна нулю. 

Шаг 1. Определите функцию

Запишите квадратичную функцию в виде f(x) = ax² + bx + c, 

где a < 0 (ветви параболы направлены вниз)

Шаг 2. Решите уравнение

Приравняйте функцию к нулю и решите уравнение ax² + bx + c = 0

Шаг 3. Найдите дискриминант

Вычислите дискриминант по формуле D = b² — 4ac

Шаг 4. Вычислите корни

Используйте формулу корней квадратного уравнения x = [-b ± √D] / (2a)

Шаг 5. Интерпретируйте результат

• x₁ (меньший корень) — нижняя точка безубыточности
• x₂ (больший корень) — верхняя точка безубыточности

Первый корень может означать минимальный порог вхождения в рынок, а второй — уровень, где затраты съедают всю прибыль. Вершина параболы будет указывать на идеальный, оптимальный размер бюджета.

Пересечение с осью Y проще всего: подставляем x = 0.

f(0) = c → точка (0, c)

В нашем примере это базовая прибыль без вложений в рекламу. Для аналитика это отправная точка, от которой начинается вся кривая и от которой удобно оценивать эффект любых изменений.

Вершина параболы

Это точка ее максимума или минимума. Она показывает оптимальное значение, например, пиковую прибыль или минимальные издержки.

Как найти вершину для квадратичной функции вида f(x) = ax² + bx + c:

• Координата x: x₀ = −b / (2a)
• Координата y: y₀ = f(x₀) (вычисляется подстановкой x₀ в функцию)

Рассмотрим на конкретном примере.

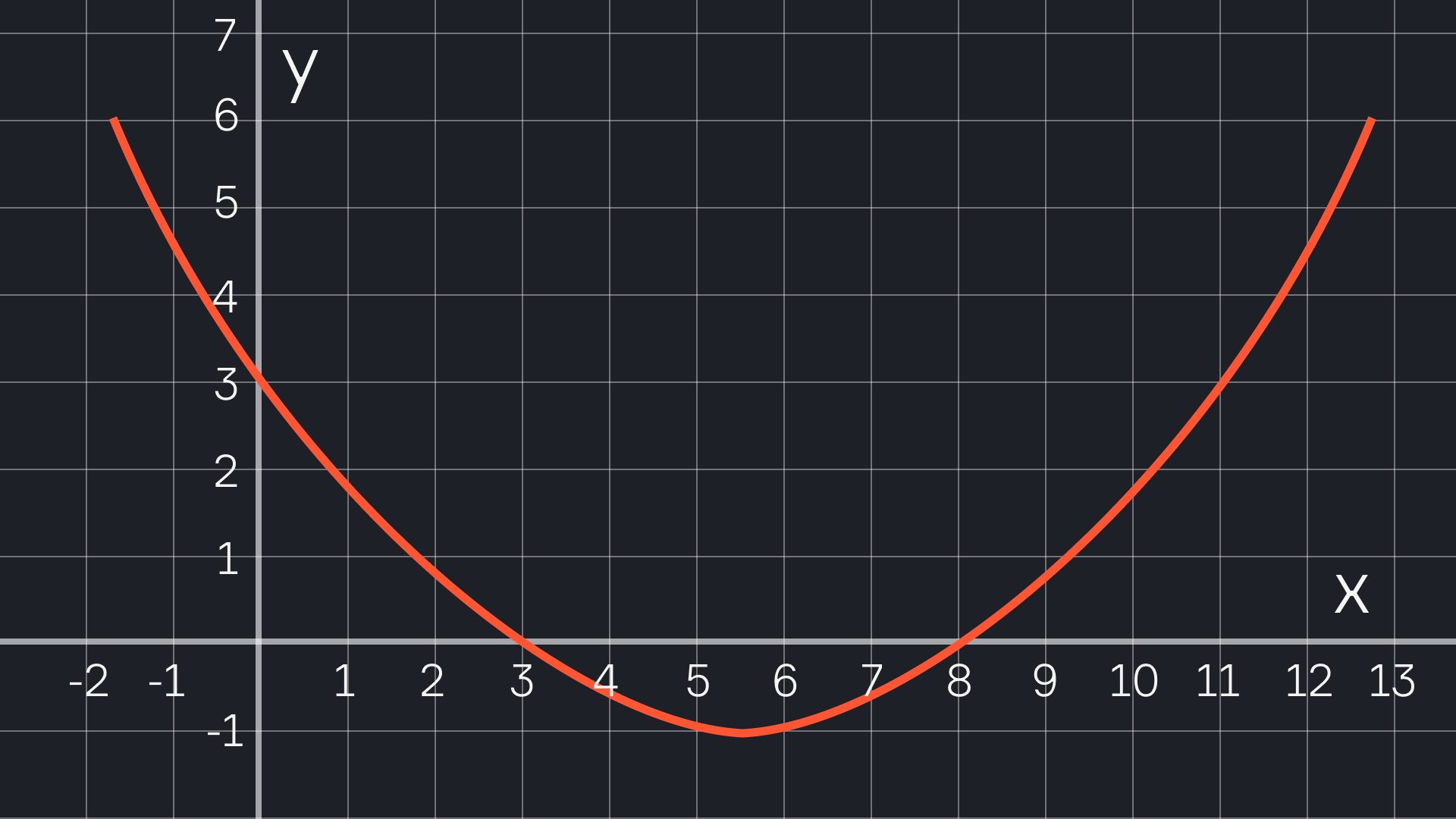
Функция прибыли: f(x) = −2x² + 8x − 1

• a = -2 → парабола направлена вниз, вершина — максимум.
• x₀ = −8 / (2 · (−2)) = 2 → оптимальный бюджет: 2 тыс. руб.
• y₀ = f(2) = −2·4 + 16 − 1 = 7 → максимальная прибыль: 7 тыс. руб.

То есть бюджет в 2 тысячи рублей обеспечивает максимальную прибыль.

Ось симметрии параболы

Это вертикальная линия, которая проходит через вершину параболы и делит ее на две зеркальные половины. На графике она помогает визуально понять, как функция ведет себя слева и справа от экстремума.

Если функция задана стандартным видом, то ось симметрии находится по формуле:

x = −b / (2a)

Значение −b/(2a) совпадает с координатой вершины, потому что именно здесь парабола достигает максимума или минимума — это центральная точка ее симметрии.

Возьмем функцию прибыли:

• f(x) = −2x² + 8x − 1
• x₀ = −8 / (2·(−2)) = 2

Ось симметрии: x = 2

Значит, что бюджеты 1 и 3 тыс. рублей дают одинаковую прибыль, как зеркальные точки относительно оптимального бюджета 2 тыс. рублей. Для аналитика это удобный способ быстро увидеть, какие варианты бюджета дадут одинаковый финансовый результат.

Алгоритм построения графика квадратичной функции

Примеры построения графиков квадратичных функций

Давайте рассмотрим два характерных примера, которые покажут универсальный алгоритм построения параболы в любой ситуации.

Пример 1: Простая парабола (a > 0)

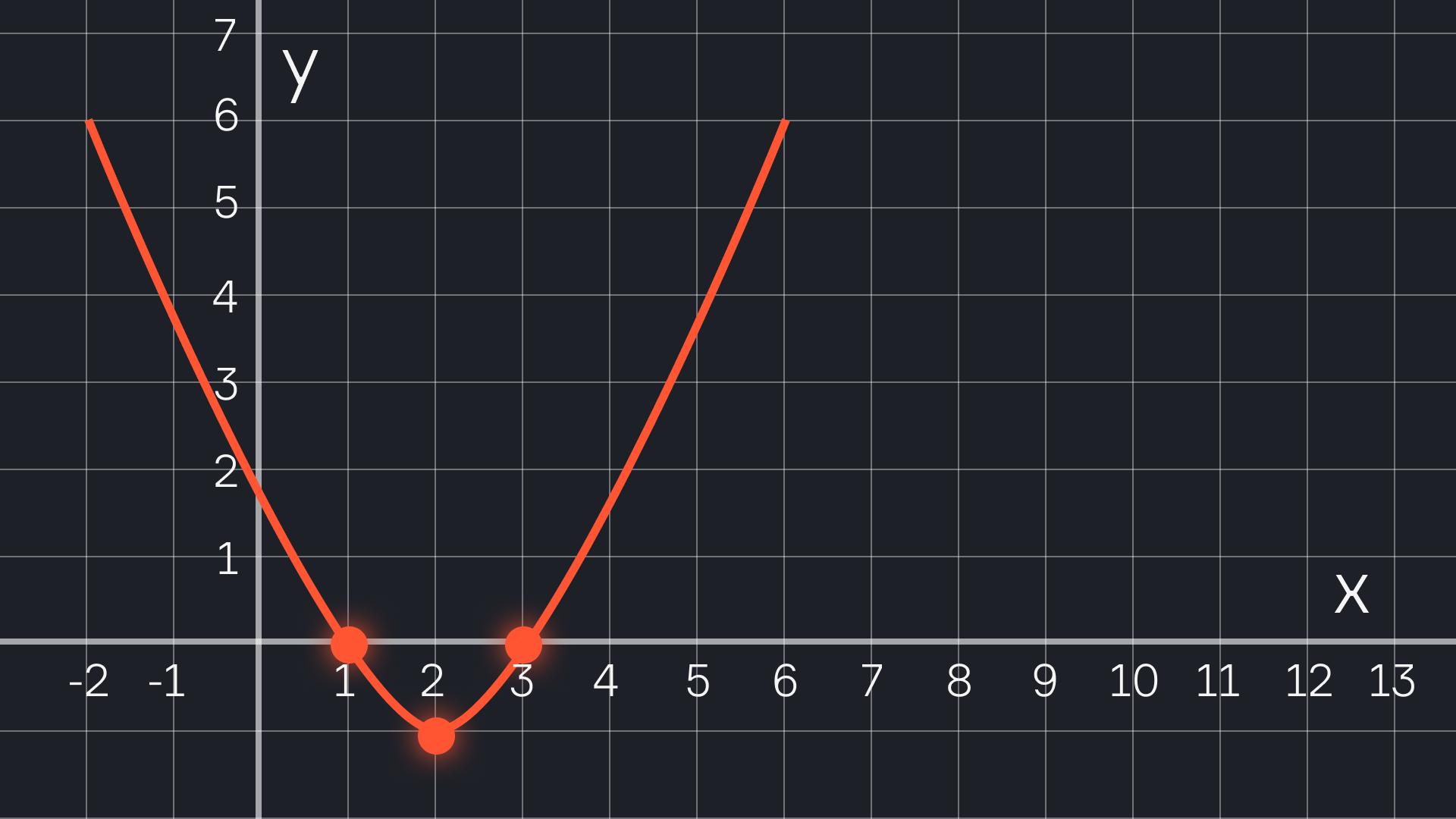
Функция: y = x² — 4x + 3

Шаг 1. Находим вершину параболы.

Абсцисса (x) вершины находится по формуле: x₀ = -b / (2a)

a = 1, b = -4

x₀ = -(-4) / (2 * 1) = 4 / 2 = 2

Теперь находим ординату (y), подставив x₀ в функцию:

y₀ = (2)² — 4*(2) + 3 = 4 — 8 + 3 = -1

Вершина: (2; -1)

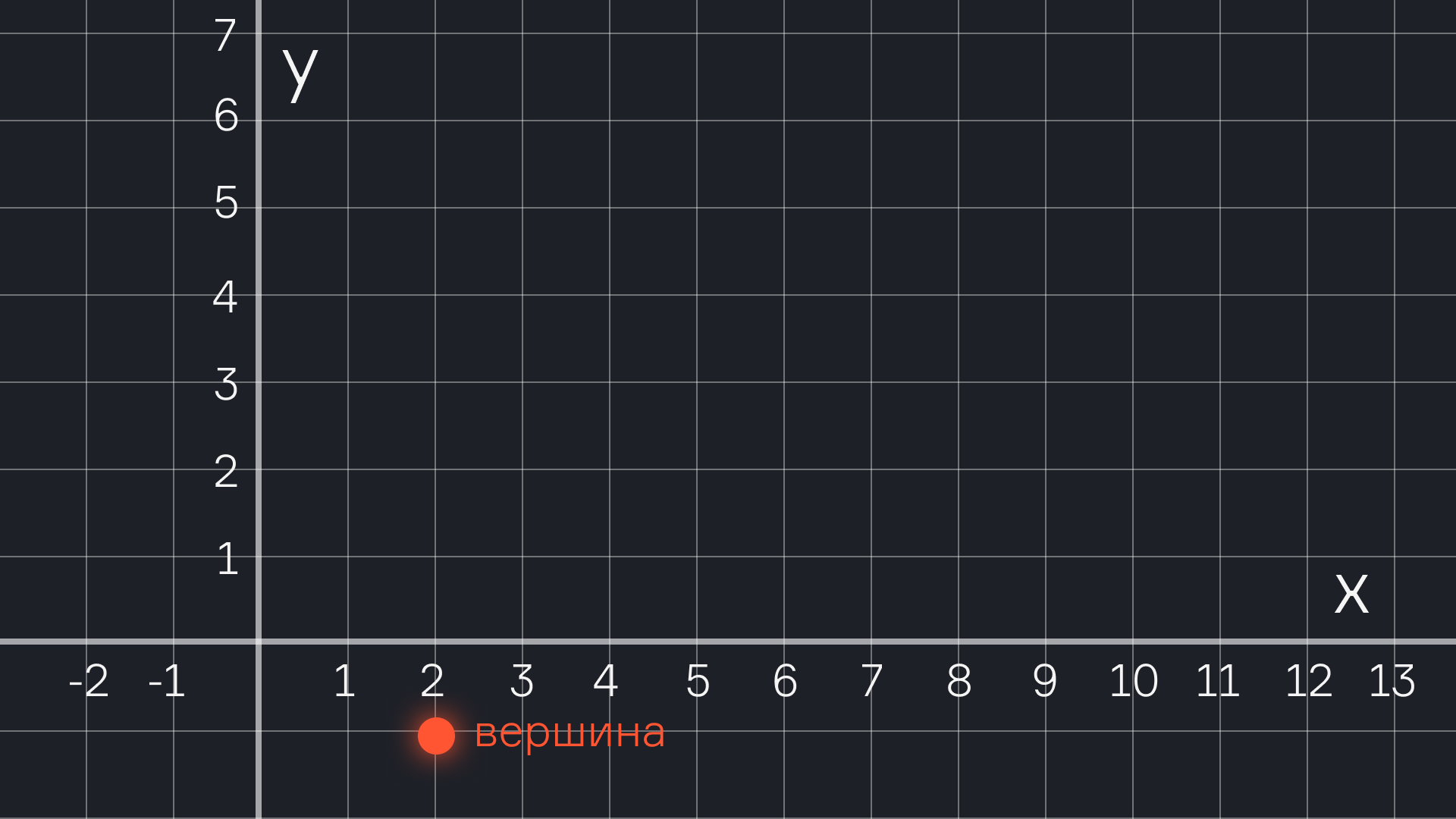
Шаг 2. Находим точки пересечения с осями.

С осью Y (x=0): y = (0)² — 4*(0) + 3 = 3 → (0; 3)

С осью X (y=0): x² — 4x + 3 = 0. Решаем квадратное уравнение:

x₁ = 1, x₂ = 3 → (1; 0) и (3; 0)

Шаг 3. Строим график по найденным точкам.

Вершина (2; -1), точки пересечения: (0; 3), (1; 0), (3; 0). Так как a=1 > 0, ветви параболы направлены вверх.

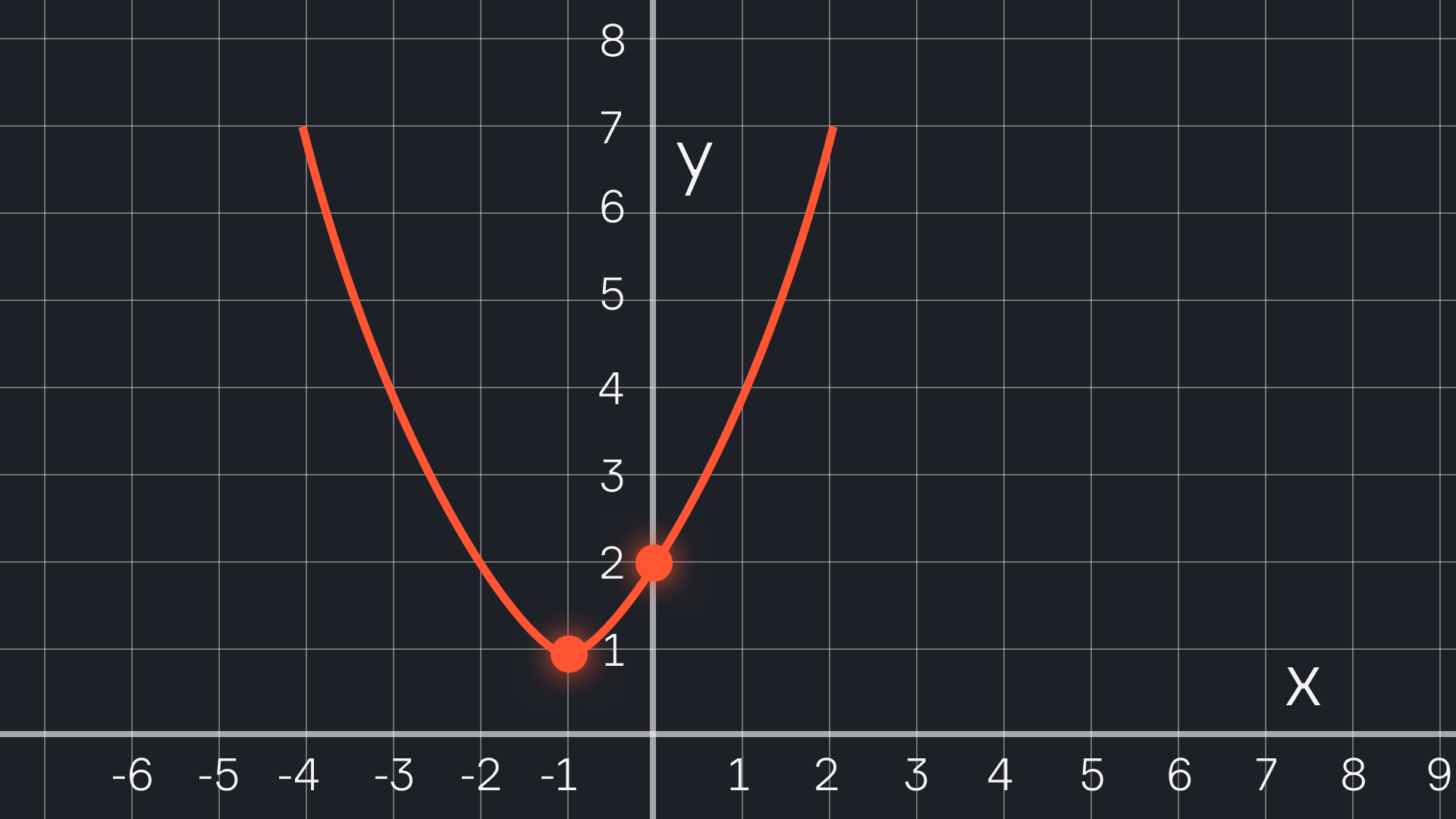
Пример 2. Парабола без действительных корней (не пересекает ось X)

Функция: y = x² + 2x + 2

Шаг 1. Находим вершину.

a = 1, b = 2

x₀ = -2 / (2 * 1) = -1

y₀ = (-1)² + 2*(-1) + 2 = 1 — 2 + 2 = 1

Вершина: (-1; 1)

Шаг 2. Находим точки пересечения с осями.

С осью Y (x=0): y = 2 → (0; 2)

С осью X (y=0): x² + 2x + 2 = 0. Дискриминант D = 4 — 8 = -4 < 0. Действительных корней нет. Парабола не пересекает ось X.

Шаг 3. Строим график.

Вершина (-1; 1), точка пересечения с Y: (0; 2). Так как a>0, ветви направлены вверх. Парабола целиком находится выше оси X.

Другие формы записи квадратичной функции

Стандартная форма удобна для быстрого чтения коэффициентов, но есть и другие варианты записи, которые решают свои задачи.

• Вершинная форма

f(x) = a(x − h)² + k

(h, k) — вершина параболы.

Подходит для быстрого построения графика и поиска экстремума.

• Факторизованная форма

f(x) = a(x − x₁)(x − x₂)

x₁ и x₂ — корни функции.

Удобна, если известны нули функции и нужно строить график через них.

Где применяется квадратичная функция в реальной жизни

Это не только школьная теория. На практике она встречается повсюду, особенно там, где показатели ведут себя нелинейно.

• Маркетинг и продажи: зависимость прибыли или конверсии от бюджета часто имеет параболическую форму.
• Оптимизация процессов: поиск максимума эффективности или минимальных затрат.
• Финансы: расчет точки безубыточности и анализ рисков.
• Физика и инженерия: движение объектов, траектории, проектирование форм.
• Data Science: моделирование нелинейных зависимостей и прогнозирование метрик.

Частые ошибки и полезные советы

Даже опытные специалисты могут допускать досадные ошибки. Разберем самые частые из них.

• Неправильно вычислить вершину.

Самая распространенная ошибка — забыть формулу x₀ = −b/(2a), что ведет к сдвигу всего графика и неверной интерпретации экстремума.

• Спутать направление ветвей.

Игнорирование знака коэффициента a приводит к принципиально неверному пониманию: там, где должен быть максимум, ищут минимум, и наоборот.

• Игнорировать ось симметрии.

Построение асимметричного графика — верный признак ошибки в расчетах. Парабола всегда симметрична относительно вертикальной прямой, проходящей через вершину.

• Неверно найти корни функции.

Особенно часто ошибаются при отрицательном дискриминанте, забывая, что в этом случае корней на оси Х нет.

• Не проверить область значений.

В бизнес-моделях это особенно важно: если прогноз выходит за разумные пределы, например, показывает отрицательные цены, такая модель уже не имеет смысла.

Полезные советы

• Всегда начинайте строить график квадратичной функции с вершины.
• Используйте ось симметрии для выбора дополнительных точек — парабола будет точной и симметричной.
• Проверяйте корни функции и пересечение с осью Y.
• Для анализа показателей сначала определяйте направление ветвей, чтобы понять, где максимум или минимум.
• Не забывайте о реальной интерпретации: цифры на графике должны соответствовать бизнес-логике и ограничениям.

Шпаргалка

Заключение 

Квадратичная функция — простой, но мощный инструмент для анализа данных. Понимание ее графика помогает аналитикам находить экстремумы, прогнозировать показатели и оптимизировать процессы без сложных вычислений.